- 🚀 Гравитационный Пинок под Космос: Как Многократные Маневры Открывают Путь к Звездам 🌌
- 🌍 Основы Гравитационных Маневров
- 📐 Методы Расчета Траекторий Многократных Гравитационных Маневров
- 🛰️ Применение Метода Сопряженных Конических Сечений
- 🧮 Численное Моделирование и Точность
- 🎯 Оптимизация Траекторий для Экономии Топлива
- 🤖 Эвристические Алгоритмы: Когда Математика Бессильна
- 🌌 Будущее Многократных Гравитационных Маневров
🚀 Гравитационный Пинок под Космос: Как Многократные Маневры Открывают Путь к Звездам 🌌
Мечтали ли вы когда-нибудь о межзвездных путешествиях? О покорении далеких галактик и исследовании неизведанных миров? Мы – да! И сегодня мы хотим поделиться с вами захватывающей темой, которая делает такие мечты все более реальными: многократные гравитационные маневры. Это не просто научная фантастика, а вполне реальный инструмент, позволяющий космическим аппаратам достигать невероятных скоростей и направляться в самые отдаленные уголки нашей Солнечной системы и за ее пределы.
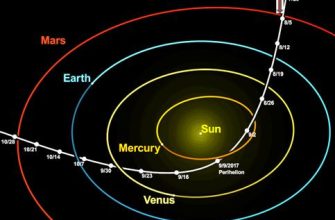
Представьте себе бильярдный шар, умело отскочивший от нескольких бортов, чтобы попасть точно в цель. Примерно так же работают гравитационные маневры, только вместо бортов используются планеты, а вместо шара – космический аппарат. Мы рассмотрим различные методы расчета этих сложных траекторий, чтобы вы могли понять, как ученые планируют эти захватывающие путешествия.
🌍 Основы Гравитационных Маневров
Гравитационный маневр, или гравитационная праща, – это использование гравитационного поля планеты для изменения скорости и направления космического аппарата. Звучит сложно, но на самом деле идея довольно проста. Когда аппарат пролетает мимо планеты, он получает "гравитационный пинок", который увеличивает или уменьшает его скорость относительно Солнца. Направление движения также меняется, позволяя аппарату лететь к другой цели.
Этот метод особенно полезен, когда требуется достичь высоких скоростей или изменить траекторию полета, не тратя при этом огромное количество топлива. Вместо того чтобы полагаться исключительно на ракетные двигатели, мы можем "одолжить" энергию у планет. Это как серфинг на гравитационных волнах!
- Увеличение скорости: Аппарат приближается к планете сзади по ее орбитальному движению.
- Уменьшение скорости: Аппарат приближается к планете спереди по ее орбитальному движению.
- Изменение направления: Траектория аппарата искривляется под воздействием гравитации планеты.
📐 Методы Расчета Траекторий Многократных Гравитационных Маневров
Расчет траекторий с использованием многократных гравитационных маневров – это сложная задача, требующая учета множества факторов. Необходимо учитывать гравитационное воздействие Солнца, планет и других небесных тел, а также ограничения, связанные с возможностями космического аппарата. Существует несколько основных методов, которые мы используем для решения этой задачи:
- Метод сопряженных конических сечений (Patched Conics): Это наиболее распространенный и относительно простой метод. Он основан на предположении, что вблизи каждой планеты аппарат движется по коническому сечению (эллипсу, параболе или гиперболе) под воздействием только гравитации этой планеты; За пределами сферы влияния планеты аппарат движется под воздействием гравитации Солнца. Эти конические сечения "сшиваются" вместе, чтобы получить общую траекторию.
- Метод численно-аналитического продолжения (Numerical Integration): Этот метод использует численные методы для интегрирования уравнений движения космического аппарата. Он позволяет учитывать гравитационное воздействие всех тел Солнечной системы, а также другие факторы, такие как сопротивление атмосферы (если аппарат находится вблизи планеты с атмосферой). Этот метод более точный, чем метод сопряженных конических сечений, но и более вычислительно сложный.
- Методы оптимального управления (Optimal Control): Эти методы используются для поиска траектории, которая минимизирует определенный критерий, например, время полета или расход топлива. Они требуют решения сложных математических задач, но позволяют получить наиболее эффективные траектории.
- Эвристические методы (Heuristic Methods): Эти методы, такие как генетические алгоритмы и методы имитации отжига, используются для поиска решений в сложных задачах, где точные методы не применимы. Они не гарантируют нахождения оптимального решения, но могут найти хорошие решения за приемлемое время.
🛰️ Применение Метода Сопряженных Конических Сечений
Метод сопряженных конических сечений – это как отправная точка в планировании межпланетных путешествий. Он позволяет нам быстро оценить возможности гравитационных маневров и определить приблизительные траектории. Хотя он и не учитывает все факторы, его простота и скорость делают его незаменимым инструментом на начальных этапах проектирования миссии.
Представьте себе, что мы планируем миссию к Юпитеру, используя гравитационный маневр у Венеры. Сначала мы рассчитываем траекторию от Земли до Венеры, затем траекторию от Венеры до Юпитера, учитывая изменение скорости и направления, полученное при пролете мимо Венеры. Затем мы "сшиваем" эти две траектории вместе, чтобы получить общую траекторию полета.
Этот метод позволяет нам быстро оценить, сколько топлива потребуется для такой миссии и сколько времени она займет. Он также помогает нам определить оптимальную дату запуска, чтобы наилучшим образом использовать гравитационное поле Венеры.
🧮 Численное Моделирование и Точность
Когда дело доходит до деталей, метод сопряженных конических сечений может быть недостаточно точным. Именно здесь на помощь приходит численное моделирование. Этот метод позволяет нам учитывать гравитационное воздействие всех тел Солнечной системы, а также другие факторы, такие как солнечный ветер и сопротивление атмосферы (если аппарат находится вблизи планеты с атмосферой).
Численное моделирование – это как создание виртуальной Солнечной системы, где мы можем "проиграть" различные сценарии полета и увидеть, как они повлияют на траекторию аппарата. Это позволяет нам точно рассчитать время и местоположение аппарата в любой момент времени, а также определить необходимые корректировки траектории.
Этот метод требует больших вычислительных ресурсов, но он обеспечивает гораздо более высокую точность, чем метод сопряженных конических сечений. Он особенно важен для миссий, требующих высокой точности, например, для посадки на поверхность планеты или для встречи с другим космическим аппаратом.
"Стремись не к успеху, а к ценностям, которые он дает." ⎯ Альберт Эйнштейн
🎯 Оптимизация Траекторий для Экономии Топлива
В космических путешествиях топливо – это золото. Чем меньше топлива мы тратим, тем дальше мы можем лететь и тем больше полезной нагрузки мы можем взять с собой. Методы оптимального управления позволяют нам найти траектории, которые минимизируют расход топлива, используя гравитационные маневры максимально эффективно.
Эти методы – это как поиск кратчайшего пути через лабиринт, где каждый поворот – это гравитационный маневр. Они требуют решения сложных математических задач, но результат стоит того. Оптимизированные траектории могут значительно сократить время полета и расход топлива, делая миссии более экономичными и осуществимыми.
Представьте себе, что мы планируем миссию к Нептуну. Без гравитационных маневров и оптимизации траектории полет может занять десятки лет и потребовать огромного количества топлива. Но, используя методы оптимального управления, мы можем найти траекторию, которая использует гравитационные поля Юпитера, Сатурна и Урана, чтобы "подтолкнуть" аппарат к Нептуну, значительно сократив время полета и расход топлива.
🤖 Эвристические Алгоритмы: Когда Математика Бессильна
Иногда задачи настолько сложны, что даже самые мощные математические методы не могут найти решение. В таких случаях мы обращаемся к эвристическим алгоритмам. Эти алгоритмы – это как умные помощники, которые используют интуицию и опыт, чтобы найти хорошие решения, даже если они не могут гарантировать, что это лучшие решения.
Генетические алгоритмы, например, имитируют процесс эволюции, создавая популяцию возможных решений и "скрещивая" их между собой, чтобы получить новые, более перспективные решения. Методы имитации отжига, в свою очередь, имитируют процесс охлаждения металла, позволяя алгоритму "выходить" из локальных оптимумов и искать более глобальные решения.
Эти методы не гарантируют нахождения оптимального решения, но они могут найти хорошие решения за приемлемое время, особенно в сложных задачах, где точные методы не применимы. Они особенно полезны для планирования миссий с множеством гравитационных маневров и сложными ограничениями.
🌌 Будущее Многократных Гравитационных Маневров
Многократные гравитационные маневры – это не просто инструмент для исследования Солнечной системы. Они могут стать ключом к межзвездным путешествиям. Представьте себе космический аппарат, который использует гравитационные поля планет и звезд, чтобы достичь невероятных скоростей и отправиться к другим звездным системам.
Конечно, это потребует разработки новых технологий и методов расчета, но мы уверены, что это возможно. Мы уже сейчас работаем над проектами, которые используют гравитационные маневры для достижения очень высоких скоростей. Возможно, в будущем мы увидим космические корабли, которые используют гравитационные поля черных дыр для путешествий в далекие галактики!
Мы верим, что многократные гравитационные маневры – это один из самых перспективных путей к освоению космоса. Они позволяют нам путешествовать дальше, быстрее и дешевле, открывая новые возможности для научных исследований и освоения новых миров. И мы с нетерпением ждем того дня, когда мы сможем отправиться в межзвездное путешествие, используя гравитационный пинок под космос!
Подробнее
| Гравитационные маневры космических аппаратов | Расчет траекторий космических полетов | Оптимизация космических миссий | Метод сопряженных конических сечений | Численное моделирование траекторий |
|---|---|---|---|---|
| Экономия топлива в космосе | Межпланетные перелеты | Гравитационная праща | Генетические алгоритмы в космонавтике | Методы оптимального управления в космосе |