Искусство Навигации: Расчет Траекторий в Мире Гравитационных Искажений

Мы, как пытливые исследователи космоса (а порой и просто разработчики игр), часто сталкиваемся с необходимостью моделировать движение объектов в сложных гравитационных полях. От точности этих расчетов зависит многое: успех космической миссии, правдоподобие игрового мира, да и просто наше понимание Вселенной. И сегодня мы хотим поделиться нашим опытом и наработками в этой увлекательной области.

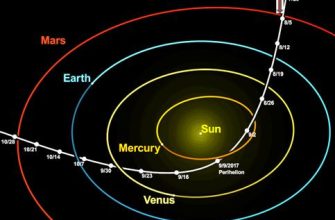
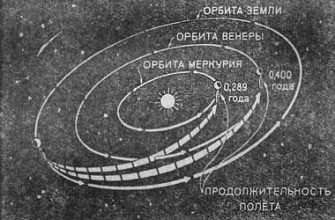
Представьте себе, что вы запускаете спутник к далекой планете. Просто рассчитать траекторию, учитывая только гравитацию центрального тела (например, Земли), – это, конечно, вариант, но он очень далек от реальности. В нашей Солнечной системе (и в любой другой, надо полагать) есть множество других тел, каждое из которых оказывает свое, пусть и небольшое, влияние на траекторию вашего спутника. Игнорирование этих "мелочей" может привести к серьезным ошибкам и даже к провалу всей миссии.

Задача расчета движения объекта под воздействием гравитации нескольких тел известна как "N-тельная задача". Она является одной из старейших и сложнейших задач небесной механики. В общем случае, для N > 2, она не имеет аналитического решения. Это означает, что мы не можем получить точную формулу, описывающую движение объекта в любой момент времени. Вместо этого нам приходится прибегать к численным методам.

Но не стоит пугаться! Численные методы – это мощный инструмент, позволяющий нам с высокой точностью моделировать движение объектов в сложных гравитационных полях. Существует множество различных численных методов, каждый из которых имеет свои достоинства и недостатки. Выбор конкретного метода зависит от требуемой точности, вычислительной мощности и специфики задачи.

Основные Методы Расчета Траекторий

Мы рассмотрим несколько основных методов, которые мы используем в нашей работе:

Метод Эйлера

Это самый простой и, пожалуй, самый интуитивно понятный численный метод. Он основан на дискретизации времени и приближении производных конечными разностями. Суть метода заключается в том, что мы вычисляем положение и скорость объекта в следующий момент времени, исходя из его положения и скорости в текущий момент времени, а также силы, действующей на объект.

Формулы метода Эйлера выглядят следующим образом:

v_i+1 = v_i + a_i * dt

r_i+1 = r_i + v_i * dt

где:

• v_i – скорость объекта в момент времени i
• a_i – ускорение объекта в момент времени i
• r_i – положение объекта в момент времени i
• dt – шаг по времени

Метод Эйлера прост в реализации, но имеет один существенный недостаток: он обладает низкой точностью. Ошибка метода накапливается с каждым шагом по времени, что может привести к значительным отклонениям от реальной траектории, особенно при больших временах моделирования. Поэтому метод Эйлера обычно используется только для грубых оценок или для задач, где не требуется высокая точность.

Метод Верле

Метод Верле – это более точный численный метод, который часто используется для моделирования движения объектов в физических системах. Он обладает хорошей стабильностью и не требует вычисления скорости на каждом шаге по времени.

Формулы метода Верле выглядят следующим образом:

r_i+1 = 2 * r_i ⎼ r_i-1 + a_i * dt²

где:

• r_i – положение объекта в момент времени i
• a_i – ускорение объекта в момент времени i
• dt – шаг по времени

Для запуска метода Верле необходимо знать положение объекта в два последовательных момента времени (r_i и r_i-1). Это можно сделать, например, с помощью метода Эйлера для первых двух шагов.

Метод Верле обеспечивает более высокую точность, чем метод Эйлера, и обладает хорошей стабильностью. Однако он не сохраняет энергию системы точно, что может привести к небольшим отклонениям от реальной траектории на больших временах моделирования.

Метод Рунге-Кутты

Методы Рунге-Кутты – это семейство численных методов для решения обыкновенных дифференциальных уравнений. Они обладают высокой точностью и стабильностью и широко используются в различных областях науки и техники, в т.ч. и для расчета траекторий.

Существует множество различных методов Рунге-Кутты, отличающихся друг от друга порядком точности и сложностью реализации. Одним из наиболее популярных является метод Рунге-Кутты 4-го порядка (RK4). Он обеспечивает высокую точность при умеренной вычислительной сложности.

Формулы метода RK4 достаточно громоздки, поэтому мы не будем приводить их здесь. Однако их можно легко найти в интернете или в учебниках по численным методам.

Методы Рунге-Кутты, особенно RK4, обеспечивают высокую точность и стабильность, что делает их хорошим выбором для расчета траекторий в сложных гравитационных полях. Однако они требуют больше вычислительных ресурсов, чем методы Эйлера и Верле.

Учет Влияния Сторонних Тел

Теперь перейдем к самому интересному – учету влияния сторонних тел. Как мы уже говорили, игнорирование этих "мелочей" может привести к серьезным ошибкам. Но как именно учитывать влияние множества гравитационных сил?

Принцип суперпозиции утверждает, что гравитационная сила, действующая на объект со стороны нескольких тел, равна векторной сумме гравитационных сил, действующих на объект со стороны каждого тела в отдельности. Это означает, что мы можем просто вычислить гравитационную силу, действующую на объект со стороны каждого тела, и затем сложить эти силы.

Формула гравитационной силы между двумя телами выглядит следующим образом:

F = G * m₁ * m₂ / r²

где:

• F – гравитационная сила
• G – гравитационная постоянная
• m₁ и m₂ – массы тел
• r – расстояние между телами

Таким образом, для учета влияния N тел на движение объекта, нам необходимо:

1. Вычислить гравитационную силу, действующую на объект со стороны каждого из N тел.
2. Сложить все эти силы, чтобы получить суммарную гравитационную силу.
3. Использовать эту суммарную силу для расчета ускорения объекта.
4. Использовать численный метод (например, метод Эйлера, Верле или Рунге-Кутты) для расчета положения и скорости объекта в следующий момент времени.

На практике, учет влияния множества тел может быть достаточно трудоемким, особенно если N велико. В таких случаях необходимо оптимизировать код и использовать эффективные алгоритмы для вычисления гравитационных сил.

Практические Советы и Рекомендации

Основываясь на нашем опыте, мы хотели бы дать несколько практических советов и рекомендаций, которые могут быть полезны при расчете траекторий с учетом влияния сторонних тел:

• Выбирайте подходящий численный метод. Метод Эйлера прост в реализации, но обладает низкой точностью. Метод Верле обеспечивает более высокую точность и стабильность. Методы Рунге-Кутты, особенно RK4, обеспечивают наивысшую точность, но требуют больше вычислительных ресурсов.
• Подбирайте оптимальный шаг по времени. Слишком большой шаг по времени может привести к неустойчивости и неточностям. Слишком маленький шаг по времени увеличивает вычислительную сложность; Оптимальный шаг по времени зависит от конкретной задачи и численного метода.
• Используйте оптимизированный код. Вычисление гравитационных сил может быть достаточно трудоемким, особенно если N велико. Используйте эффективные алгоритмы и оптимизированный код для ускорения расчетов.
• Проверяйте результаты. Всегда проверяйте результаты расчетов на соответствие физическим законам и здравому смыслу. Сравнивайте результаты с другими источниками, если это возможно.
• Учитывайте погрешности. Любые численные методы имеют погрешности. Учитывайте эти погрешности при анализе результатов.

Примеры Использования

Рассмотрим несколько примеров использования методов расчета траекторий с учетом влияния сторонних тел:

Моделирование Движения Спутников

Расчет траекторий спутников вокруг Земли требует учета влияния не только Земли, но и Луны, Солнца и других планет. Точный расчет траектории необходим для поддержания спутника на заданной орбите и для предотвращения столкновений с другими космическими объектами.

Моделирование Движения Планет

Моделирование движения планет в Солнечной системе требует учета влияния всех планет, а также Солнца. Точный расчет траекторий необходим для прогнозирования будущих положений планет и для изучения эволюции Солнечной системы.

Создание Реалистичных Игровых Миров

В компьютерных играх часто требуется моделировать движение объектов в гравитационных полях. Учет влияния множества тел может сделать игровой мир более реалистичным и интересным.

Расчет траекторий с учетом влияния сторонних тел – это сложная, но увлекательная задача. Она требует знания численных методов, понимания физических законов и умения программировать. Однако, освоив эти навыки, вы сможете моделировать движение объектов в сложных гравитационных полях и создавать реалистичные игровые миры.

Мы надеемся, что наша статья была полезной и интересной. Желаем вам успехов в ваших исследованиях!

Подробнее

Численное моделирование траекторий	Гравитационное взаимодействие тел	Метод Эйлера для траекторий	Метод Верле в астрономии	Метод Рунге-Кутты для орбит
Влияние гравитации планет	Расчет траектории спутника	N-тельная задача решение	Моделирование движения тел	Оптимизация расчета траекторий