Искусство Управления Полeтом: Методы Расчета Траекторий с Учетом Управляемых Импульсов

Мы, как энтузиасты в области моделирования и управления движением, часто сталкиваемся с задачей расчета траекторий. Это не просто набор математических формул, а целое искусство, требующее понимания физики, математики и, конечно же, умения применять современные вычислительные методы. В этой статье мы погрузимся в мир расчета траекторий с учетом управляемых импульсов, рассмотрим различные подходы и поделимся нашим опытом.

Представьте себе, что вы управляете космическим кораблем, летящим к далекой звезде. Каждый импульс двигателя – это изменение скорости, которое влияет на вашу траекторию. Как рассчитать эти импульсы так, чтобы достичь цели оптимальным образом? Это и есть суть задачи, которую мы будем решать.

Основы Расчета Траекторий

Расчет траекторий начинается с понимания основных законов движения. Мы используем законы Ньютона, уравнения Эйлера и другие математические инструменты для описания движения объекта в пространстве. Важно учитывать не только силу тяги двигателей, но и гравитационные силы, аэродинамическое сопротивление (если речь идет о полете в атмосфере) и другие факторы.

На практике это означает, что мы строим математическую модель, которая описывает положение и скорость объекта в каждый момент времени. Эта модель может быть очень сложной, особенно если мы учитываем множество факторов.

Управляемые Импульсы: Что Это Такое?

Управляемые импульсы – это изменения скорости объекта, которые мы можем контролировать. В случае космического корабля, это включение и выключение двигателей. Каждый импульс имеет величину (изменение скорости) и направление. Выбор правильных импульсов – это ключ к оптимальной траектории.

Представьте себе, что вы играете в бильярд. Удар кием – это импульс, который вы придаете шару. Правильно рассчитанный удар позволит вам забить шар в лузу. Аналогично, правильно рассчитанные импульсы позволят нам доставить объект к цели с минимальными затратами.

Методы Расчета Траекторий с Учетом Управляемых Импульсов

Существует множество методов расчета траекторий с учетом управляемых импульсов. Мы рассмотрим наиболее распространенные и эффективные из них.

Метод Лагранжа

Метод Лагранжа – это классический подход, основанный на минимизации функционала действия. Мы строим функцию Лагранжа, которая описывает энергию системы, и затем ищем экстремум этой функции. Решение этой задачи дает нам оптимальную траекторию.

Этот метод особенно полезен для задач с ограничениями, например, когда мы должны учитывать ограничения на топливо или время полета.

Метод оптимального управления

Метод оптимального управления – это более современный подход, основанный на принципе максимума Понтрягина. Мы формулируем задачу как задачу оптимизации, в которой мы хотим минимизировать некоторый критерий (например, расход топлива) при заданных ограничениях.

Этот метод позволяет решать сложные задачи, в которых необходимо учитывать нелинейные эффекты и ограничения.

Численные Методы

В большинстве реальных задач аналитическое решение найти невозможно. В этом случае мы используем численные методы, такие как метод Рунге-Кутты или метод Эйлера. Эти методы позволяют нам приближенно решать уравнения движения и находить оптимальные траектории.

Численные методы требуют больших вычислительных ресурсов, но они позволяют решать задачи любой сложности.

Применение Методов на Практике

Мы применяли эти методы для решения различных задач, от управления движением роботов до расчета траекторий космических аппаратов. В каждом случае мы сталкивались с уникальными проблемами и находили творческие решения.

Например, при разработке системы управления движением робота-манипулятора нам пришлось учитывать ограничения на скорость и ускорение двигателей. Мы использовали метод оптимального управления для нахождения траектории, которая минимизирует время выполнения задачи при заданных ограничениях.

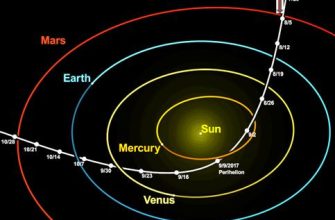
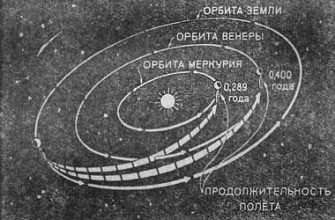
Пример: Расчет Траектории Космического Аппарата

Рассмотрим пример расчета траектории космического аппарата, летящего к Марсу. Мы хотим найти траекторию, которая минимизирует расход топлива и время полета.

Для этого мы используем метод оптимального управления. Мы строим математическую модель, которая описывает движение аппарата в гравитационном поле Солнца и планет. Затем мы формулируем задачу оптимизации, в которой мы хотим минимизировать суммарный импульс двигателей при заданных ограничениях на время полета.

Решение этой задачи дает нам оптимальную траекторию, которая позволяет доставить аппарат к Марсу с минимальными затратами.

Проблемы и Решения

Расчет траекторий с учетом управляемых импульсов – это сложная задача, которая связана с рядом проблем. Мы рассмотрим наиболее распространенные из них и поделимся нашим опытом по их решению.

Вычислительная Сложность

Численные методы требуют больших вычислительных ресурсов, особенно для сложных задач. Для решения этой проблемы мы используем современные вычислительные методы и алгоритмы, такие как параллельные вычисления и методы оптимизации.

Неопределенность

В реальных задачах всегда присутствует неопределенность, связанная с погрешностями измерений и моделирования. Для учета неопределенности мы используем методы робастного управления и адаптивного управления.

Ограничения

В большинстве задач существуют ограничения, например, на топливо, время полета или углы ориентации. Для учета ограничений мы используем методы оптимального управления и методы математического программирования.

Расчет траекторий с учетом управляемых импульсов – это увлекательная и сложная задача, которая требует глубоких знаний в области физики, математики и вычислительной техники. Мы надеемся, что эта статья помогла вам лучше понять основные методы и подходы к решению этой задачи.

Мы продолжаем исследовать новые методы и подходы к расчету траекторий и будем рады поделиться нашими результатами с вами.

Дополнительные Материалы

Для тех, кто хочет углубиться в эту тему, мы рекомендуем ознакомиться со следующими материалами:

• Книги по теории оптимального управления
• Статьи в научных журналах по аэрокосмической тематике
• Онлайн-курсы по моделированию и управлению движением

Также, вам может быть полезно изучить следующие темы:

1. Вариационное исчисление
2. Принцип максимума Понтрягина
3. Методы численного интегрирования дифференциальных уравнений

Подробнее

Колонка 1	Колонка 2	Колонка 3	Колонка 4	Колонка 5
Оптимизация траектории полета	Управление космическим кораблем	Расчет импульсов двигателя	Метод Лагранжа в космонавтике	Численное моделирование траекторий
Оптимальное управление движением	Траектории с минимальным расходом	Принцип максимума Понтрягина	Робастное управление полетом	Адаптивное управление движением