Как мы покоряли "Тундру": Расчет траекторий спутников – от теории к практике

Приветствую, друзья! Сегодня мы хотим поделиться с вами захватывающим опытом, который стал для нас настоящим вызовом и одновременно невероятно интересным приключением. Речь пойдет о расчете траекторий для спутников, работающих на орбитах типа "Тундра". Это не просто сухие математические выкладки и сложные алгоритмы. Это история о том, как мы пытались заглянуть в будущее движения космических аппаратов, предсказать их положение и обеспечить стабильную связь с Землей. Готовы отправиться с нами в это космическое путешествие?

Работа с орбитами "Тундра" – это всегда компромисс между сложностью и эффективностью. Эти орбиты позволяют спутникам проводить большую часть времени над определенной территорией, что делает их незаменимыми для задач связи и наблюдения. Но за эту "привилегию" приходится платить – сложностью расчета траекторий и необходимостью учитывать множество факторов, влияющих на движение спутника. Давайте разберемся, с какими трудностями мы столкнулись и как их преодолевали.

Что такое орбита "Тундра" и почему она так важна?

Орбита "Тундра" – это высокоэллиптическая орбита, наклоненная к экватору Земли под углом около 63.4 градусов. Особенность этой орбиты в том, что спутник проводит большую часть своего времени вблизи апогея (самой удаленной точки от Земли) над определенным районом земной поверхности. Это достигается за счет того, что скорость спутника в апогее значительно ниже, чем в перигее (самой близкой точке к Земле). Благодаря этому, спутники на орбите "Тундра" обеспечивают длительное время непрерывного покрытия нужной территории, что критически важно для многих приложений.

Представьте себе, что вам нужно обеспечить постоянную связь с удаленным регионом, например, с северными районами России. Использование геостационарных спутников в данном случае неэффективно из-за низкого угла места и больших потерь сигнала. А вот спутник на орбите "Тундра", "зависающий" над этой территорией, – идеальное решение. Именно поэтому орбиты "Тундра" широко используются в системах спутниковой связи, навигации и наблюдения за Землей.

Сложности расчета траекторий: гравитация, атмосфера и не только

Расчет траекторий спутников – это сложная задача, требующая учета множества факторов. Основным из них, конечно, является гравитационное поле Земли. Однако, гравитация – это не просто сила притяжения сферически симметричной массы. Земля имеет сложную форму, ее гравитационное поле неоднородно, и это оказывает существенное влияние на траекторию спутника. Кроме того, необходимо учитывать гравитационное воздействие Луны и Солнца, особенно на высоких орбитах.

Другим важным фактором является сопротивление атмосферы. Хотя на высотах орбит "Тундра" атмосфера очень разрежена, она все же оказывает влияние на движение спутника, постепенно замедляя его и снижая высоту орбиты. Величина сопротивления атмосферы зависит от множества факторов, таких как плотность атмосферы, форма и размеры спутника, его ориентация в пространстве. Точное определение этих параметров – задача нетривиальная.

Наши инструменты и методы: от классики до современных решений

Для расчета траекторий мы использовали как классические методы небесной механики, так и современные программные комплексы. Начинали мы, конечно, с решения задачи двух тел – классической задачи Кеплера. Однако, для достижения необходимой точности, пришлось учитывать возмущения от гравитационного поля Земли, Луны, Солнца и сопротивления атмосферы. Для этого мы использовали методы численного интегрирования уравнений движения, такие как метод Рунге-Кутты.

В качестве программного обеспечения мы использовали как коммерческие пакеты, так и собственные разработки. Среди коммерческих пакетов особенно хочется отметить STK (Satellite Tool Kit), который предоставляет широкие возможности для моделирования космических миссий и расчета траекторий. В то же время, мы разработали собственные алгоритмы и программы для решения специфических задач, таких как оптимизация траектории и анализ чувствительности к различным параметрам.

Практические примеры и сложности, с которыми мы столкнулись

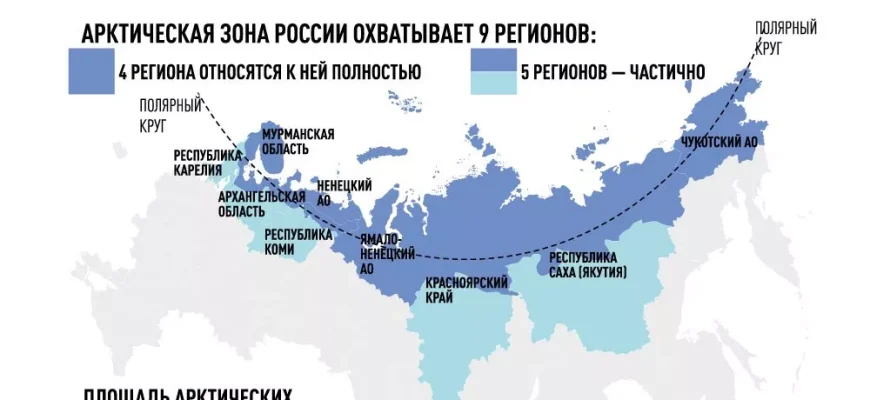
Одним из самых интересных проектов, в которых мы участвовали, был расчет траектории для спутника связи, предназначенного для работы в Арктической зоне. Задачей было обеспечить максимальное время непрерывного покрытия территории с минимальным количеством спутников. Решение оказалось нетривиальным, и нам пришлось перебрать множество вариантов орбит, прежде чем мы нашли оптимальное решение.

В процессе работы мы столкнулись с рядом сложностей. Во-первых, это высокая чувствительность траектории к начальным условиям. Небольшая ошибка в определении начальной позиции или скорости спутника могла привести к существенным отклонениям от расчетной траектории. Во-вторых, это сложность моделирования атмосферного сопротивления. Плотность атмосферы сильно зависит от солнечной активности, которую сложно предсказать с высокой точностью. В-третьих, это вычислительные затраты. Численное интегрирование уравнений движения требует значительных вычислительных ресурсов, особенно при моделировании длительных периодов времени.

Оптимизация траекторий: как добиться максимальной эффективности

Оптимизация траекторий – это искусство поиска наилучшего компромисса между различными параметрами, такими как время покрытия, потребляемая мощность, точность наведения и стоимость. Для решения этой задачи мы использовали различные методы оптимизации, такие как генетические алгоритмы, метод имитации отжига и метод роя частиц.

Генетические алгоритмы оказались особенно эффективными для поиска глобального оптимума в многомерном пространстве параметров. Суть метода заключается в имитации процесса эволюции, когда популяция "особей" (в нашем случае, вариантов орбит) подвергается селекции, скрещиванию и мутации. В результате, популяция постепенно "эволюционирует" в направлении оптимума.

Проверка и корректировка: как обеспечить точность прогноза

Даже самый точный расчет траектории нуждается в проверке и корректировке. В процессе эксплуатации спутника его фактическая траектория может отклоняться от расчетной из-за различных факторов, таких как ошибки в определении параметров, неточности моделирования и внешние воздействия. Для корректировки траектории используются специальные двигатели, которые позволяют изменять скорость и направление движения спутника.

Мы использовали различные методы для отслеживания траектории спутника и определения необходимых корректировок. Одним из наиболее эффективных методов является использование данных телеметрии, получаемых с Земли. Анализируя эти данные, можно определить текущее положение и скорость спутника, а также оценить величину отклонения от расчетной траектории. На основе этой информации формируются команды для двигателей корректировки, которые позволяют вернуть спутник на заданную траекторию.

Работа с расчетом траекторий для спутников на орбитах типа "Тундра" стала для нас ценным опытом. Мы убедились в том, что это сложная, но в то же время невероятно интересная задача, требующая глубоких знаний в области небесной механики, математики и программирования. Мы научились учитывать множество факторов, влияющих на движение спутника, использовать различные методы оптимизации и корректировки траектории.

Наш опыт показывает, что для успешного решения подобных задач необходимо сочетать теоретические знания с практическими навыками, использовать современные программные инструменты и постоянно совершенствовать свои знания. Мы надеемся, что наш опыт будет полезен для тех, кто только начинает свой путь в этой увлекательной области.

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
Орбита Тундра применение	Расчет траекторий спутников	Параметры орбиты Тундра	Программное обеспечение для расчета траекторий	Моделирование космических миссий
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
Оптимизация орбит спутников	Влияние атмосферы на орбиту спутника	Корректировка траектории спутника	Гравитационные возмущения на орбите	Спутниковая связь в Арктике