Магия орбит: Как рассчитать траекторию, когда космос полон сюрпризов

Когда мы смотрим на ночное небо, усыпанное звездами, легко забыть, что за кажущейся простотой скрывается сложная и динамичная система. Планеты вращаются вокруг Солнца, спутники кружат вокруг планет, а астероиды и кометы путешествуют по своим собственным, часто непредсказуемым, путям. Каждый из этих объектов оказывает гравитационное воздействие на другие, делая расчет траекторий невероятно сложной задачей. Именно об этом мы и поговорим сегодня – о том, как мы, люди, научились предсказывать эти движения, учитывая все эти "космические сюрпризы".

Понимание и прогнозирование траекторий небесных тел – это не просто академический интерес. Это критически важно для множества практических применений, от запуска спутников и космических зондов до предотвращения столкновений с астероидами. Представьте себе, что было бы, если бы мы не могли точно рассчитать траекторию космического корабля, направляющегося к Марсу! Цена ошибки была бы огромной. Поэтому давайте углубимся в эту захватывающую область и разберемся, какие методы мы используем для решения этих головоломок.

Основы небесной механики

Прежде чем мы погрузимся в сложные методы расчета траекторий, нам необходимо понять основные принципы, лежащие в основе небесной механики. В первую очередь, это законы Кеплера, которые описывают движение планет вокруг Солнца. Эти законы, сформулированные еще в начале 17-го века, заложили фундамент для нашего понимания орбит. Они гласят, что планеты движутся по эллиптическим орбитам, Солнце находится в одном из фокусов эллипса, а скорость движения планеты меняется в зависимости от ее положения на орбите.

Но законы Кеплера – это только начало. Для более точных расчетов необходимо учитывать закон всемирного тяготения Ньютона. Этот закон гласит, что сила гравитационного притяжения между двумя телами пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Именно благодаря этому закону мы можем объяснить, почему планеты остаются на своих орбитах и почему спутники вращаются вокруг планет. Однако, когда мы имеем дело с множеством тел, взаимодействующих друг с другом, ситуация становится гораздо сложнее.

Задача N тел

Проблема, с которой мы сталкиваемся при расчете траекторий в реальном космосе, известна как "задача N тел". Суть ее в том, что аналитическое решение существует только для задачи двух тел (например, планета и звезда). Когда мы добавляем третье тело (например, другой планеты или спутника), уравнения становятся настолько сложными, что их невозможно решить аналитически. В таких случаях мы прибегаем к численным методам.

Численные методы – это способы приближенного решения уравнений движения с помощью компьютера. Они включают в себя разбиение времени на небольшие интервалы и последовательное вычисление положения и скорости каждого тела на каждом шаге. Чем меньше интервал времени, тем точнее результат, но тем больше вычислительных ресурсов требуется. Существует множество различных численных методов, каждый из которых имеет свои преимущества и недостатки. Выбор конкретного метода зависит от требуемой точности и доступных вычислительных ресурсов.

Методы учета влияния сторонних тел

Теперь давайте перейдем к самой интересной части – как мы учитываем влияние "сторонних тел" при расчете траекторий. Существует несколько подходов к решению этой задачи, каждый из которых имеет свои особенности и ограничения.

Метод возмущений

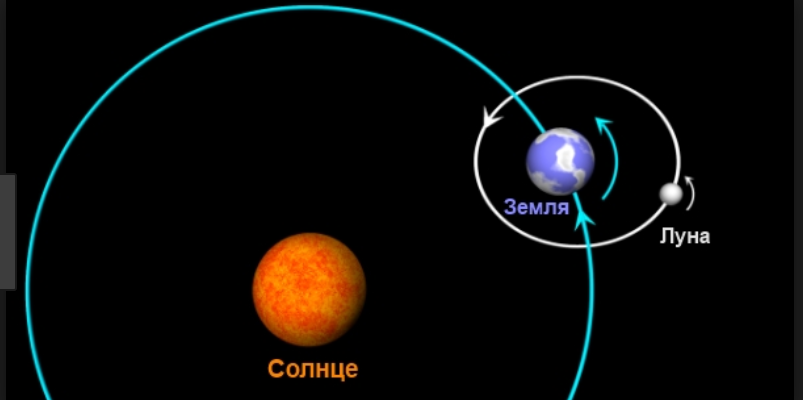
Одним из наиболее распространенных методов является метод возмущений. Идея заключается в том, что мы сначала рассчитываем траекторию тела, пренебрегая влиянием всех остальных тел, а затем вносим поправки (возмущения), учитывающие их гравитационное воздействие. Этот метод хорошо работает, когда возмущения относительно малы, то есть когда гравитационное влияние сторонних тел не слишком велико. Например, его можно использовать для расчета траектории спутника, вращающегося вокруг Земли, учитывая влияние Луны и Солнца.

Метод возмущений может быть реализован различными способами, в зависимости от требуемой точности и сложности задачи. Одним из наиболее распространенных подходов является использование рядов Фурье для представления возмущений. Это позволяет нам разложить сложные возмущения на более простые компоненты, которые можно легко вычислить. Однако этот метод может быть вычислительно затратным, особенно если требуется высокая точность.

Метод N-тельного моделирования

Когда влияние сторонних тел становится значительным, метод возмущений может оказаться недостаточно точным. В таких случаях мы прибегаем к методу N-тельного моделирования. Этот метод заключается в прямом численном решении уравнений движения для всех тел, участвующих в гравитационном взаимодействии. Это самый точный, но и самый вычислительно затратный метод. Он требует огромных вычислительных ресурсов, особенно когда количество тел велико.

Метод N-тельного моделирования широко используется в астрофизике для моделирования формирования галактик, звездных скоплений и планетных систем. Он позволяет нам изучать сложные гравитационные взаимодействия и предсказывать эволюцию этих систем. Однако его применение ограничено вычислительными возможностями. Для моделирования больших систем с большим количеством тел требуются суперкомпьютеры.

Метод ограниченной задачи трех тел

Метод ограниченной задачи трех тел – это упрощенный вариант задачи N тел, который позволяет нам изучать движение третьего тела (например, спутника или астероида) в гравитационном поле двух массивных тел (например, Земли и Луны). В этом методе мы предполагаем, что масса третьего тела пренебрежимо мала по сравнению с массами двух других тел, и что оно не оказывает существенного влияния на их движение.

Метод ограниченной задачи трех тел позволяет нам аналитически или численно изучать движение третьего тела и определять области, в которых оно может оставаться на стабильной орбите. Эти области, известные как точки Лагранжа, представляют особый интерес для космических миссий, так как они позволяют нам размещать спутники, требующие минимального количества топлива для поддержания своей орбиты.

Практическое применение методов расчета траекторий

Теперь, когда мы рассмотрели основные методы расчета траекторий с учетом влияния сторонних тел, давайте посмотрим, как они применяются на практике.

Запуск и управление спутниками

Одной из наиболее важных областей применения этих методов является запуск и управление спутниками. Точный расчет траектории спутника необходим для того, чтобы он достиг заданной орбиты и оставался на ней в течение всего срока службы. При этом необходимо учитывать влияние Земли, Луны, Солнца и других спутников, а также сопротивление атмосферы.

• Расчет траектории вывода: Определение оптимального пути ракеты-носителя для вывода спутника на заданную орбиту.
• Поддержание орбиты: Коррекция траектории спутника для компенсации возмущений и поддержания его на заданной орбите.
• Уклонение от космического мусора: Расчет траекторий космического мусора и маневрирование спутника для предотвращения столкновений.

Межпланетные перелеты

Еще одним важным применением методов расчета траекторий является планирование межпланетных перелетов. Для того чтобы космический корабль достиг другой планеты, необходимо точно рассчитать его траекторию, учитывая гравитационное влияние Солнца, Земли, Луны и других планет. Это сложная задача, требующая использования высокоточных численных методов и большого количества вычислительных ресурсов.

1. Расчет траектории перелета: Определение оптимального пути космического корабля от Земли до другой планеты.
2. Гравитационный маневр: Использование гравитационного поля планет для изменения скорости и направления движения космического корабля.
3. Коррекция траектории: Внесение небольших изменений в траекторию космического корабля для компенсации ошибок и достижения заданной цели.

Предотвращение столкновений с астероидами

Методы расчета траекторий также используются для предотвращения столкновений с астероидами. Постоянно ведется мониторинг околоземных астероидов, и ученые рассчитывают их траектории, чтобы определить, представляют ли они угрозу для Земли. Если обнаруживается астероид, который может столкнуться с Землей, разрабатываются планы по изменению его траектории, например, с помощью ядерного взрыва или гравитационного трактора.

Параметр	Описание	Значение
Название астероида	Идентификатор астероида в базе данных	(101955) Bennu
Диаметр	Приблизительный диаметр астероида	500 метров
Вероятность столкновения	Вероятность столкновения с Землей в течение определенного периода	1/2700 (в период с 2175 по 2199 год)
Методы отклонения	Рассматриваемые методы для изменения траектории астероида	Кинетический удар, гравитационный трактор, ядерный взрыв

Будущее методов расчета траекторий

Область расчета траекторий постоянно развивается. С развитием вычислительной техники и появлением новых алгоритмов мы можем решать все более сложные задачи и получать все более точные результаты. В будущем мы можем ожидать следующих достижений:

• Более точные модели гравитационного поля: Улучшение моделей гравитационного поля Земли, Луны и других планет для повышения точности расчетов.
• Новые численные методы: Разработка новых численных методов, которые будут более эффективными и точными.
• Использование искусственного интеллекта: Применение искусственного интеллекта для автоматизации процесса расчета траекторий и оптимизации параметров космических миссий.

Например, машинное обучение может помочь в оптимизации траекторий космических аппаратов, учитывая множество факторов, таких как расход топлива, время полета и гравитационные возмущения. Это позволит нам осуществлять более сложные и эффективные космические миссии, открывая новые горизонты для исследования космоса.

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
расчет траектории космического аппарата	влияние гравитации на траекторию	численные методы небесной механики	траектория полета к Марсу	моделирование движения небесных тел
прогнозирование орбит спутников	гравитационное воздействие планет	алгоритмы расчета траекторий	динамика космического полета	метод возмущений в небесной механике