Межпланетные Путешествия: Как мы рассчитываем траектории к далеким мирам

Мечта о покорении космоса всегда жила в человечестве. Мы, как и многие, с замиранием сердца следим за каждым новым шагом в освоении Вселенной; И, пожалуй, один из самых захватывающих аспектов космических миссий – это планирование траекторий полета к другим планетам. Как вообще возможно отправить космический аппарат в другую часть Солнечной системы, чтобы он достиг своей цели? Это сложная задача, требующая глубоких знаний в математике, физике и астрономии. В этой статье мы расскажем о том, как мы, увлеченные космическими исследованиями, разбираемся в этих сложных вычислениях и какие принципы лежат в основе расчета траекторий для миссий к внешним планетам.

Основы межпланетных траекторий: гравитация и законы Кеплера

Прежде чем углубляться в сложные алгоритмы, важно понять основы. В космосе все подчиняется законам гравитации, сформулированным Исааком Ньютоном. Эти законы описывают взаимодействие между объектами, обладающими массой. Планеты вращаются вокруг Солнца не просто так – их удерживает его мощное гравитационное поле. Кроме того, движение планет подчиняется законам Кеплера, которые описывают форму орбит (эллипсы), скорость движения по орбите и связь между периодом обращения и размером орбиты.

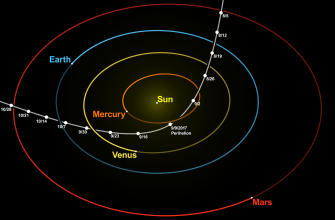
Мы часто представляем себе космический полет как прямую линию от Земли к, скажем, Марсу. Но в реальности это было бы невероятно энергозатратно. Гораздо эффективнее использовать так называемые перелетные траектории, которые позволяют космическому аппарату "скользить" по гравитационным полям планет, экономя топливо и время.

Гравитационные маневры: использование гравитации планет

Гравитационный маневр – это как космический бильярд! Мы "подлетаем" к планете, используя ее гравитацию, чтобы изменить скорость и направление полета космического аппарата. Представьте себе, что вы бросаете мячик в сторону движущегося поезда. Если мячик пролетит достаточно близко, поезд немного изменит его траекторию и скорость. То же самое происходит и в космосе, только вместо поезда у нас планета, а вместо мячика – космический аппарат.

Мы используем гравитационные маневры для достижения нескольких целей:

Увеличение скорости: Подлетая к планете "сзади", космический аппарат получает дополнительный импульс от ее гравитации.
Изменение направления: Пролетая мимо планеты под определенным углом, можно изменить направление полета без использования топлива.
Коррекция траектории: Небольшие гравитационные маневры позволяют точно настроить траекторию и компенсировать ошибки, возникшие в процессе полета.

Расчет траекторий: математические модели и программное обеспечение

Расчет межпланетных траекторий – это сложная математическая задача. Мы используем различные математические модели, учитывающие гравитационное влияние Солнца, планет и других небесных тел. Эти модели позволяют нам предсказывать движение космического аппарата с высокой точностью.

Для расчетов мы используем специализированное программное обеспечение, которое позволяет:

Моделировать гравитационные поля планет и других небесных тел.
Рассчитывать траектории полета с учетом гравитационных маневров.
Оптимизировать траектории для минимизации затрат топлива и времени.
Визуализировать траектории в трехмерном пространстве.

Пример используемого программного обеспечения:

Название программы	Описание
STK (Satellite Tool Kit)	Мощный инструмент для моделирования космических миссий и анализа траекторий.
GMAT (General Mission Analysis Tool)	Бесплатное программное обеспечение, разработанное NASA, для проектирования и анализа космических миссий.

"Космос – это не просто место, куда мы отправляемся. Это вызов, который формирует нас." ౼ Нил Деграсс Тайсон

Факторы, влияющие на выбор траектории

Выбор оптимальной траектории для миссии к внешней планете зависит от множества факторов. Мы учитываем:

Положение планет: Планеты постоянно движутся, поэтому их взаимное расположение меняется со временем. Мы должны выбрать момент запуска, когда планеты находятся в наиболее выгодной конфигурации для полета.
Запас топлива: Чем меньше топлива требуется для достижения цели, тем больше полезной нагрузки можно взять на борт космического аппарата.
Время полета: Длительные полеты увеличивают риск поломок оборудования и подвергают экипаж воздействию космической радиации.
Научные цели миссии: Траектория должна позволять выполнить все запланированные научные исследования.
Ограничения по аппаратуре: Грузоподъемность ракеты-носителя, энергопотребление и другие параметры аппаратуры влияют на выбор траектории.

Примеры миссий к внешним планетам

Рассмотрим несколько примеров успешных миссий к внешним планетам, демонстрирующих различные подходы к расчету траекторий:

"Вояджер-1" и "Вояджер-2": Эти аппараты использовали гравитационные маневры у Юпитера, Сатурна, Урана и Нептуна, чтобы исследовать внешнюю Солнечную систему. "Вояджер-2" – единственный аппарат, посетивший Уран и Нептун;
"Кассини-Гюйгенс": Этот аппарат исследовал Сатурн и его спутники. Траектория включала несколько гравитационных маневров у Венеры, Земли и Юпитера.
"Новые горизонты": Этот аппарат пролетел мимо Плутона и пояса Койпера. Траектория была оптимизирована для максимально быстрого достижения Плутона.

Будущее межпланетных путешествий

Мы уверены, что будущее межпланетных путешествий полно захватывающих возможностей. Развитие новых технологий, таких как ионные двигатели и солнечные паруса, позволит нам создавать более эффективные и быстрые космические аппараты. Мы также работаем над разработкой новых методов расчета траекторий, которые позволят нам достигать самых отдаленных уголков Солнечной системы и за ее пределами.

Мечта о полете к звездам становится все ближе. И мы рады быть частью этого удивительного процесса.

Подробнее

Межпланетные перелеты	Гравитационные маневры	Космические траектории	Миссии к планетам	Законы Кеплера
Расчет орбит	Космическое топливо	Программное обеспечение для космоса	Полет к Марсу	Исследование космоса