Межпланетные странствия: Как мы рассчитываем траектории для космических зондов

Межпланетные путешествия – это не просто захватывающие истории из научной фантастики․ Это сложнейшие инженерные и научные задачи, требующие невероятной точности и глубокого понимания законов физики․ Как же мы, скромные исследователи космоса, отправляем зонды к другим планетам? Какие вычисления стоят за каждым успешным полетом? Позвольте нам рассказать об этом увлекательном процессе․

В этой статье мы погрузимся в мир расчетов траекторий для межпланетных зондов, рассмотрим основные принципы, методы и инструменты, которые мы используем․ Мы поделимся опытом, расскажем о трудностях, с которыми сталкиваемся, и о том, как их преодолеваем․ Приготовьтесь к путешествию в мир небесной механики и космической инженерии!

Основы межпланетных траекторий

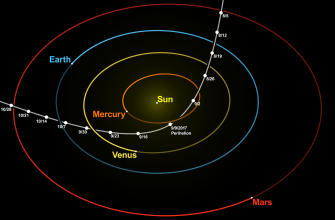
Межпланетные траектории – это не прямые линии․ Зонд не может просто "включить двигатели" и полететь к Марсу по кратчайшему пути․ На движение космического аппарата влияют гравитационные поля Солнца, Земли, других планет и даже крупных астероидов․ Поэтому мы используем гравитацию этих тел, чтобы "подтолкнуть" зонд в нужном направлении, экономя топливо и время․

Основным принципом, лежащим в основе большинства межпланетных траекторий, является гравитационный маневр․ Он заключается в том, что зонд пролетает мимо планеты на определенном расстоянии и использует её гравитационное поле для изменения своей скорости и направления движения․ Этот метод позволяет значительно сократить расход топлива, так как для изменения траектории используется "бесплатная" энергия гравитации․

Другой важный аспект – это выбор оптимального времени старта․ Планеты постоянно движутся по своим орбитам, и расстояние между ними постоянно меняется․ Существуют определенные "окна запуска", когда положение планет наиболее благоприятно для полета к цели с минимальными затратами энергии․ Эти окна рассчитываются заранее с использованием сложных математических моделей․

Методы расчета траекторий

Для расчета межпланетных траекторий мы используем различные методы, каждый из которых имеет свои преимущества и недостатки․ Выбор метода зависит от конкретной задачи, требуемой точности и доступных ресурсов․

Метод конических сечений

Это один из самых простых и распространенных методов․ Он основан на предположении, что движение зонда между двумя планетами происходит по коническому сечению (эллипсу, параболе или гиперболе) под действием гравитации только одного тела – Солнца․ Этот метод позволяет получить приблизительное решение достаточно быстро, но не учитывает влияние других планет, что снижает его точность․

Метод численного интегрирования

Этот метод более точный, чем метод конических сечений․ Он заключается в численном решении уравнений движения зонда, учитывающих гравитационное воздействие всех значимых тел в Солнечной системе․ Этот метод требует больших вычислительных ресурсов, но позволяет получить более точные результаты, особенно для длительных полетов․

Метод оптимального управления

Этот метод используется для поиска траектории, которая минимизирует определенный критерий, например, расход топлива или время полета․ Он основан на принципах оптимального управления и требует решения сложных математических задач․ Этот метод позволяет найти наиболее эффективные траектории, но требует значительных вычислительных ресурсов и времени․

Инструменты для расчета траекторий

Для расчета межпланетных траекторий мы используем специализированное программное обеспечение, разработанное для решения задач небесной механики и космической динамики․ Вот некоторые из наиболее распространенных инструментов:

STK (Satellite Tool Kit) – мощный коммерческий инструмент, используемый для моделирования и анализа космических миссий․
GMAT (General Mission Analysis Tool) – бесплатный инструмент, разработанный NASA, для проектирования и оптимизации космических миссий․
Orekit – бесплатная библиотека на Java для расчета орбит и траекторий космических аппаратов․
собственные разработки ― часто мы разрабатываем собственные инструменты и алгоритмы, адаптированные под конкретные задачи и требования миссии․

Эти инструменты позволяют нам моделировать движение зонда, учитывать влияние различных факторов, оптимизировать траекторию и оценивать риски․

"Космос – это не предел․ Это вызов․"

– Артур Кларк

Трудности и вызовы

Расчет межпланетных траекторий – это сложная задача, сопряженная с рядом трудностей и вызовов․ Вот некоторые из них:

Неопределенность параметров․ Мы не всегда можем точно знать положение и скорость планет, массу и форму астероидов, параметры атмосферы и поверхности планет․ Эта неопределенность может привести к ошибкам в расчетах и потребовать внесения коррекций в траекторию в процессе полета․
Влияние малых сил․ На движение зонда могут влиять малые силы, такие как давление солнечного света, гравитационное воздействие Луны и других небольших тел․ Учет этих сил требует сложных математических моделей и больших вычислительных ресурсов․
Ограничения по ресурсам․ Зонд имеет ограниченный запас топлива, энергии и времени․ Мы должны оптимизировать траекторию, чтобы достичь цели с минимальными затратами ресурсов․
Отказы оборудования․ В процессе полета могут произойти отказы оборудования, что потребует внесения изменений в траекторию и программу миссии․

Преодоление этих трудностей требует от нас высокой квалификации, опыта и творческого подхода․ Мы постоянно разрабатываем новые методы и алгоритмы, чтобы повысить точность и надежность расчетов․

Примеры успешных миссий

Несмотря на все трудности, мы успешно отправляем зонды к другим планетам и получаем ценные научные данные․ Вот несколько примеров успешных миссий, траектории которых были рассчитаны с использованием современных методов:

Voyager 1 и Voyager 2 – две легендарные миссии, запущенные в 1977 году, которые исследовали Юпитер, Сатурн, Уран и Нептун, используя гравитационные маневры․
Cassini-Huygens – миссия к Сатурну, запущенная в 1997 году, которая достигла Сатурна в 2004 году и исследовала планету, ее кольца и спутники в течение 13 лет․
Rosetta – миссия к комете 67P/Чурюмова-Герасименко, запущенная в 2004 году, которая достигла кометы в 2014 году и сбросила на ее поверхность спускаемый аппарат Philae․
New Horizons – миссия к Плутону, запущенная в 2006 году, которая пролетела мимо Плутона в 2015 году и получила первые детальные снимки планеты․

Эти миссии демонстрируют, что сложные межпланетные путешествия возможны благодаря точному расчету траекторий и использованию современных технологий․

Будущее межпланетных путешествий

Межпланетные путешествия – это не только научные исследования, но и перспектива освоения других планет и создания внеземных колоний․ В будущем мы планируем отправлять все более сложные и амбициозные миссии, например:

Миссии к Европе и Титану – спутникам Юпитера и Сатурна, на которых, возможно, существует жизнь․
Миссии по возврату образцов грунта с Марса – для поиска следов прошлой или настоящей жизни․
Миссии по колонизации Марса – для создания первого внеземного поселения․

Реализация этих планов потребует разработки новых технологий и методов расчета траекторий, а также сотрудничества между различными странами и организациями․ Но мы уверены, что будущее межпланетных путешествий будет ярким и захватывающим․

Мы надеемся, что эта статья помогла вам понять, как мы рассчитываем траектории для межпланетных зондов․ Это сложная, но увлекательная задача, требующая глубоких знаний, опыта и творческого подхода․ Мы гордимся тем, что вносим свой вклад в исследование космоса и приближаем будущее межпланетных путешествий․

Подробнее

Межпланетные полеты	Траектории космических аппаратов	Гравитационный маневр	Расчет орбит	Космическая навигация
Программное обеспечение для расчета траекторий	Оптимизация траекторий	Миссии к Марсу	Исследование Солнечной системы	Небесная механика