Навигация в Космосе: Как Сторонние Тела Меняют Курс?

Космические путешествия всегда казались нам чем-то невероятно сложным и захватывающим. И это действительно так! Когда мы запускаем ракету в космос, мы не просто отправляем её в пустоту. Мы отправляем её в сложную гравитационную игру, где каждый объект – планета, луна, астероид – оказывает своё влияние. Игнорирование этих влияний может привести к катастрофическим последствиям. Нам, как инженерам и исследователям космоса, постоянно приходится учитывать эти факторы при расчете траекторий космических аппаратов.

В этой статье мы погрузимся в мир расчетов траекторий, учитывающих влияние сторонних тел. Мы расскажем о методах, которые используем, о сложностях, с которыми сталкиваемся, и о том, как современные технологии помогают нам решать эти задачи. Готовьтесь к захватывающему путешествию в мир небесной механики!

Основы небесной механики: Гравитация и траектории

Прежде чем углубиться в сложные расчеты, давайте вспомним основы. Все началось с Исаака Ньютона и его закона всемирного тяготения. Этот закон гласит, что любое тело притягивает другое тело с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Звучит просто, но именно это простое уравнение лежит в основе всей небесной механики.

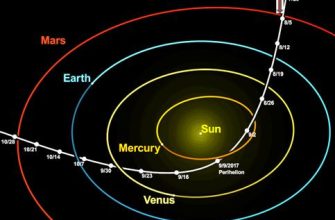
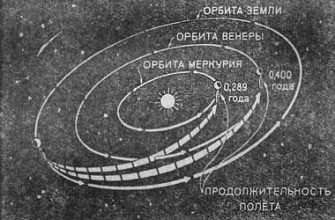
Когда мы рассматриваем движение космического аппарата вокруг одного тела (например, Земли), его траектория описывается коническим сечением: окружностью, эллипсом, параболой или гиперболой. Форма траектории зависит от начальной скорости и энергии аппарата. Однако в реальном космосе все гораздо сложнее. На аппарат воздействуют гравитационные силы не только Земли, но и Луны, Солнца, других планет и даже астероидов. Именно учет этих "сторонних тел" превращает простую задачу в невероятно сложную.

Задача N тел: Неразрешимая сложность?

Ситуация, когда на тело воздействуют гравитационные силы нескольких других тел, называется "задачей N тел". К сожалению, для N > 2 не существует общего аналитического решения этой задачи. Это означает, что мы не можем написать формулу, которая описывала бы движение тела в такой системе. Вместо этого мы вынуждены использовать численные методы – приближенные вычисления, которые позволяют нам с достаточной точностью предсказать траекторию.

Численные методы – это основа современной космической навигации. Они позволяют нам моделировать движение космического аппарата с учетом гравитационного влияния всех значимых тел в Солнечной системе. Однако эти методы требуют огромных вычислительных ресурсов и очень чувствительны к начальным условиям. Небольшая ошибка в начальной скорости или положении аппарата может привести к значительному отклонению от предсказанной траектории через некоторое время.

Методы расчета траекторий с учетом влияния сторонних тел

Существует несколько основных методов, которые мы используем для расчета траекторий с учетом влияния сторонних тел. Каждый из них имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи.

Метод Эйлера: Простота и ограничения

Метод Эйлера – самый простой численный метод для решения дифференциальных уравнений. Он заключается в том, что мы разбиваем время на небольшие интервалы и на каждом интервале считаем, что ускорение аппарата постоянно. Используя это приближение, мы можем вычислить изменение скорости и положения аппарата за каждый интервал.

Метод Эйлера прост в реализации, но имеет низкую точность. Ошибка накапливается с каждым шагом, и через некоторое время результат может сильно отличаться от реальной траектории. Поэтому метод Эйлера обычно используется только для предварительных расчетов или для задач, где не требуется высокая точность.

Метод Рунге-Кутты: Точность и скорость

Методы Рунге-Кутты – это семейство более точных численных методов для решения дифференциальных уравнений. Они используют несколько промежуточных точек внутри каждого временного интервала для более точной оценки изменения скорости и положения аппарата. Существует несколько вариантов методов Рунге-Кутты разного порядка точности. Наиболее распространенным является метод Рунге-Кутты 4-го порядка, который обеспечивает хороший баланс между точностью и вычислительной сложностью.

Методы Рунге-Кутты широко используются в космической навигации благодаря своей высокой точности и относительной скорости. Они позволяют нам моделировать траектории космических аппаратов с достаточной точностью для большинства задач.

Метод многошаговых методов Адамса: Эффективность и стабильность

Многошаговые методы Адамса используют значения скорости и положения аппарата на нескольких предыдущих временных шагах для вычисления его положения на следующем шаге; Это позволяет им достичь высокой точности при меньшем количестве вычислений, чем методы Рунге-Кутты. Однако многошаговые методы требуют запуска с использованием одношагового метода (например, метода Рунге-Кутты) для получения начальных значений.

Многошаговые методы Адамса особенно эффективны для задач, где требуется высокая точность и скорость вычислений, например, для моделирования долгосрочных траекторий космических аппаратов.

Факторы, влияющие на точность расчетов траекторий

Точность расчетов траекторий зависит от множества факторов; Учет этих факторов позволяет нам повысить надежность и безопасность космических миссий.

Точность определения положения и скорости небесных тел

Чем точнее мы знаем положение и скорость небесных тел, тем точнее мы можем рассчитать гравитационное воздействие, которое они оказывают на космический аппарат. Поэтому мы постоянно совершенствуем методы определения положения и скорости планет, лун и астероидов. Для этого используются радиолокационные наблюдения, оптические телескопы и данные, полученные с других космических аппаратов.

Точность модели гравитационного поля Земли (и других планет)

Гравитационное поле Земли не является однородным. Оно имеет сложную структуру, обусловленную неоднородным распределением массы внутри Земли. Для точного расчета траекторий космических аппаратов необходимо учитывать эти неоднородности. Для этого используются сложные модели гравитационного поля, которые строятся на основе данных, полученных с гравитационных спутников.

Влияние атмосферы

Атмосфера Земли оказывает сопротивление движению космических аппаратов, особенно на низких орбитах. Это сопротивление приводит к замедлению аппарата и снижению его орбиты. Для точного расчета траекторий необходимо учитывать влияние атмосферы. Для этого используются модели атмосферы, которые учитывают изменение плотности и температуры воздуха в зависимости от высоты и времени суток.

Солнечное давление

Солнечный свет оказывает давление на космические аппараты. Это давление очень мало, но на больших расстояниях от Земли оно может оказать существенное влияние на траекторию. Для точного расчета траекторий необходимо учитывать солнечное давление. Для этого необходимо знать площадь поверхности аппарата и его отражательные свойства.

Релятивистские эффекты

Вблизи массивных тел (например, Солнца) необходимо учитывать релятивистские эффекты, предсказанные общей теорией относительности Эйнштейна. Эти эффекты приводят к искривлению пространства-времени и изменению траектории космического аппарата. Релятивистские эффекты особенно важны для миссий, которые проходят вблизи Солнца.

Применение расчетов траекторий в космических миссиях

Расчеты траекторий с учетом влияния сторонних тел играют ключевую роль во всех этапах космической миссии – от планирования до управления полетом.

Планирование миссии

На этапе планирования миссии мы используем расчеты траекторий для определения оптимальной траектории полета к цели. Мы учитываем гравитационное влияние всех значимых тел в Солнечной системе, чтобы минимизировать расход топлива и время полета. Также мы учитываем ограничения, связанные с видимостью цели, возможностью связи с Землей и другими факторами.

Управление полетом

Во время полета мы постоянно отслеживаем траекторию космического аппарата и сравниваем ее с предсказанной. Если обнаруживаются отклонения, мы вносим корректировки в траекторию с помощью двигателей. Расчеты траекторий с учетом влияния сторонних тел позволяют нам точно определить, какие корректировки необходимо внести, чтобы вернуть аппарат на заданный курс.

Коррекция траектории

Коррекция траектории – это процесс внесения изменений в траекторию космического аппарата с помощью двигателей. Коррекции траектории необходимы для компенсации ошибок, связанных с неточностью начальных условий, воздействием атмосферы, солнечным давлением и другими факторами. Расчеты траекторий с учетом влияния сторонних тел позволяют нам точно рассчитать величину и направление импульса, необходимого для коррекции траектории.

Будущее расчетов траекторий

Область расчетов траекторий постоянно развивается. С появлением новых технологий и улучшением понимания физических процессов мы можем делать расчеты все более точными и эффективными.

Использование искусственного интеллекта

Искусственный интеллект (ИИ) может быть использован для автоматизации процесса расчета траекторий и оптимизации параметров миссии. ИИ может анализировать большие объемы данных и выявлять закономерности, которые не видны человеку. Также ИИ может быть использован для разработки более точных моделей гравитационного поля и атмосферы.

Разработка новых численных методов

Продолжаеться разработка новых численных методов для решения задачи N тел. Эти методы должны быть более точными, быстрыми и устойчивыми к ошибкам. Особое внимание уделяется разработке методов, которые могут работать с большими системами, содержащими множество тел.

Квантовые вычисления

Квантовые компьютеры могут революционизировать область расчетов траекторий. Они могут решать задачи, которые не под силу классическим компьютерам. В частности, квантовые компьютеры могут быть использованы для решения задачи N тел с высокой точностью и скоростью.

Расчет траекторий с учетом влияния сторонних тел – это сложная и важная задача, которая играет ключевую роль в успехе космических миссий. Мы, как специалисты в этой области, постоянно работаем над улучшением методов расчетов и повышением точности предсказаний. Использование новых технологий, таких как искусственный интеллект и квантовые вычисления, открывает новые возможности для исследования космоса.

Надеемся, что эта статья помогла вам понять, как мы ориентируемся в космосе и как учитываем влияние всех окружающих нас тел. Космос полон сюрпризов, и мы всегда должны быть готовы к новым вызовам!

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
гравитационное воздействие планет	численное моделирование траекторий	методы коррекции траектории	расчет траекторий космических аппаратов	влияние солнечного давления на траекторию
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
небесная механика и космические полеты	алгоритмы расчета траекторий	точность определения орбит	оптимизация траекторий космических миссий	моделирование гравитационного поля Земли