Орбитальные Танцы: Как Рассчитать Маневры Изменения Орбиты и Не Упасть в Космос

Когда мы смотрим на звезды‚ часто забываем о сложной хореографии‚ происходящей вокруг нашей планеты. Спутники‚ космические корабли‚ даже МКС – все они постоянно корректируют свои траектории‚ чтобы оставаться на своих заданных орбитах. Эти корректировки‚ или маневры изменения орбиты‚ требуют точных расчетов и понимания фундаментальных законов физики. Сегодня мы погрузимся в этот захватывающий мир‚ чтобы разобраться‚ как эти маневры рассчитываются и какие факторы необходимо учитывать. Мы расскажем о нашем опыте и знаниях‚ накопленных в этой области‚ чтобы вы могли лучше понять‚ как космические аппараты "танцуют" в космосе.

Основы Орбитальной Механики: Краткий Обзор

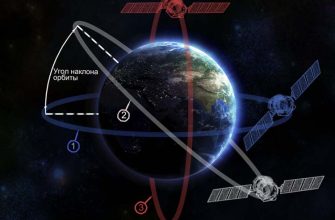
Прежде чем мы начнем говорить о маневрах‚ важно понимать основы орбитальной механики. Орбита – это путь‚ по которому объект движется вокруг другого объекта под действием гравитации. В нашем случае‚ это обычно Земля и спутник или космический корабль. Форма орбиты может быть круглой или эллиптической‚ и она определяется несколькими ключевыми параметрами‚ такими как большая полуось‚ эксцентриситет и наклонение. Эти параметры‚ в свою очередь‚ влияют на скорость и положение объекта на орбите.

Одним из самых важных понятий является закон сохранения энергии. Он гласит‚ что полная механическая энергия орбиты остается постоянной. Это означает‚ что изменение скорости объекта приводит к изменению его высоты над Землей и‚ соответственно‚ к изменению его потенциальной энергии. Понимание этого закона критически важно для расчета маневров изменения орбиты.

Зачем Вообще Нужны Маневры Изменения Орбиты?

Маневры изменения орбиты необходимы по множеству причин. Во-первых‚ реальные орбиты редко бывают идеальными. Возмущения‚ вызванные гравитацией Луны‚ Солнца‚ неоднородностью гравитационного поля Земли и даже сопротивлением атмосферы (для низких орбит)‚ постоянно отклоняют спутники от их запланированных траекторий. Во-вторых‚ иногда требуется изменить орбиту для выполнения определенных задач. Например‚ для перехода с одной орбиты на другую‚ для сближения с другим космическим аппаратом или для возвращения на Землю.

Приведем несколько примеров:

• Коррекция орбиты: Поддержание спутника на заданной орбите для обеспечения стабильного покрытия связью или наблюдения.
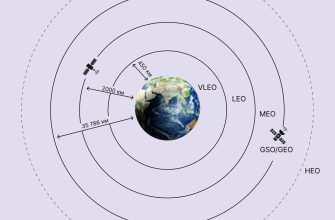
• Переход на другую орбиту: Достижение геостационарной орбиты (GEO) с геопереходной орбиты (GTO).
• Сближение и стыковка: Маневры‚ необходимые для стыковки космических кораблей‚ например‚ с МКС.
• Уклонение от космического мусора: Изменение орбиты для избежания столкновения с опасными объектами.

Типы Маневров Изменения Орбиты: От Простого к Сложному

Существует множество типов маневров изменения орбиты‚ каждый из которых предназначен для решения определенных задач. Самые простые маневры – это импульсные маневры‚ когда двигатель включается на короткое время‚ чтобы мгновенно изменить скорость объекта. Более сложные маневры включают непрерывное включение двигателя в течение длительного времени.

Импульсные Маневры: Быстро и Эффективно?

Импульсные маневры – это‚ пожалуй‚ самый распространенный тип маневров. Они основаны на кратковременном включении двигателя‚ которое приводит к мгновенному изменению скорости. Это изменение скорости обозначается как ΔV (дельта-V) и является ключевым параметром при расчете маневров. Чем больше ΔV требуется для маневра‚ тем больше топлива необходимо потратить.

Вот несколько примеров импульсных маневров:

• Маневр Гомана: Самый энергоэффективный способ перехода между двумя круговыми орбитами‚ лежащими в одной плоскости.
• Биэллиптический переход: Более сложный маневр‚ который может быть более эффективным‚ чем маневр Гомана‚ при больших изменениях радиуса орбиты.
• Изменение наклонения: Маневр‚ который изменяет угол между плоскостью орбиты и экватором Земли.

Непрерывные Маневры: Медленно‚ но Верно

Непрерывные маневры‚ в отличие от импульсных‚ предполагают постоянное включение двигателя в течение длительного времени. Этот тип маневров часто используется для коррекции орбиты или для поддержания положения спутника в определенной точке пространства. Примером непрерывного маневра может служить коррекция орбиты геостационарного спутника‚ который постоянно подвергается воздействию гравитационных возмущений.

Расчет ΔV: Основа для Планирования Маневров

Расчет ΔV – это‚ пожалуй‚ самый важный этап в планировании любого маневра изменения орбиты. ΔV определяет‚ сколько топлива потребуется для выполнения маневра‚ и‚ следовательно‚ влияет на массу космического аппарата и его стоимость. Существуют различные формулы и методы для расчета ΔV‚ в зависимости от типа маневра и параметров орбиты.

Для маневра Гомана‚ например‚ ΔV можно рассчитать по следующей формуле:

ΔV = sqrt(μ/r₁) * (sqrt(2r₂/(r₁ + r₂)) ⏤ 1) + sqrt(μ/r₂) (1 ౼ sqrt(2*r₁/(r₁ + r₂)))

Где:

• μ – гравитационный параметр Земли
• r₁ – радиус начальной орбиты
• r₂ – радиус конечной орбиты

Эта формула показывает‚ что ΔV зависит от разницы между радиусами начальной и конечной орбит. Чем больше эта разница‚ тем больше ΔV потребуется для выполнения маневра.

Факторы‚ Влияющие на Расчет Маневров: От Атмосферы до Космического Мусора

Расчет маневров изменения орбиты – это не просто применение формул. Необходимо учитывать множество факторов‚ которые могут повлиять на точность расчетов и эффективность маневра. Эти факторы можно разделить на несколько категорий:

1. Гравитационные возмущения: Гравитация Луны‚ Солнца и неоднородность гравитационного поля Земли.
2. Атмосферное сопротивление: Особенно важно для низких орбит.
3. Космический мусор: Риск столкновения с мусором требует маневров уклонения.
4. Точность двигателей: Неточности в работе двигателей могут потребовать дополнительных корректировок.

Учет этих факторов требует использования сложных математических моделей и алгоритмов. Современные системы управления космическими аппаратами используют компьютерное моделирование и оптимизацию для планирования маневров‚ учитывающих все эти факторы.

Практические Примеры: От МКС до Межпланетных Перелетов

Маневры изменения орбиты используются в самых разных космических миссиях. Рассмотрим несколько примеров:

• МКС: МКС регулярно выполняет маневры коррекции орбиты‚ чтобы компенсировать атмосферное сопротивление и поддерживать свою высоту.
• Геостационарные спутники: Геостационарные спутники постоянно выполняют маневры‚ чтобы оставаться в своей "точке стояния" над Землей.
• Межпланетные перелеты: Перелеты к другим планетам требуют сложных маневров изменения орбиты‚ использующих гравитационную помощь планет для экономии топлива.

Каждый из этих примеров требует уникального набора маневров и точных расчетов. Успех этих миссий зависит от тщательного планирования и выполнения этих маневров.

Будущее Орбитальных Маневров: Новые Технологии и Подходы

Область орбитальных маневров постоянно развивается. Разрабатываются новые технологии и подходы‚ которые позволяют выполнять маневры более эффективно и точно. Некоторые из этих технологий включают:

• Ионные двигатели: Обеспечивают очень высокую эффективность использования топлива‚ но имеют малую тягу;
• Гравитационные маневры: Использование гравитации планет для изменения скорости и направления космического аппарата.
• Автономное управление: Разработка систем‚ которые позволяют космическим аппаратам самостоятельно планировать и выполнять маневры.

Эти новые технологии открывают новые возможности для исследования космоса и использования космического пространства.

Расчет маневров изменения орбиты – это сложная и важная задача‚ которая лежит в основе многих космических миссий. Понимание принципов орбитальной механики‚ умение рассчитывать ΔV и учитывать различные факторы‚ влияющие на орбиту‚ – все это необходимо для успешного освоения космоса. Мы надеемся‚ что эта статья помогла вам лучше понять‚ как космические аппараты "танцуют" в космосе и какие усилия требуются для поддержания этой сложной хореографии.

Подробнее

Орбитальный маневр	Изменение орбиты	Расчет траектории	Космический полет	Дельта V
Гравитационный маневр	Коррекция орбиты	Спутниковая орбита	Космическая навигация	Механика полета