От хаоса к порядку: Укрощение траекторий численным интегрированием

Мы, как исследователи и энтузиасты, часто сталкиваемся с необходимостью моделировать и предсказывать поведение сложных систем. Будь то движение планет, траектория ракеты или даже изменение цен на акции, в основе всего этого лежат дифференциальные уравнения. Но что делать, если аналитическое решение получить невозможно? Здесь на помощь приходят методы численного интегрирования – наши верные помощники в мире приближенных вычислений.

В этой статье мы погрузимся в увлекательный мир численного интегрирования траекторий. Мы рассмотрим основные методы, их преимущества и недостатки, а также области применения. Приготовьтесь к путешествию, полному математических формул, алгоритмов и практических советов!

Зачем нужно численное интегрирование траекторий?

Представьте себе, что вам нужно рассчитать траекторию полета мяча, брошенного под углом к горизонту. В идеальном мире, без учета сопротивления воздуха, это довольно простая задача, решаемая аналитически. Но что, если учитывать сопротивление воздуха, которое зависит от скорости мяча, его формы и других факторов? Уравнение движения становится настолько сложным, что аналитическое решение найти практически невозможно.

Именно в таких случаях на помощь приходит численное интегрирование. Оно позволяет нам получить приближенное решение дифференциального уравнения, разбивая время на небольшие шаги и вычисляя положение и скорость объекта на каждом шаге. Таким образом, мы можем построить траекторию движения, даже если аналитическое решение недоступно.

Численное интегрирование траекторий широко используется в самых разных областях, таких как:

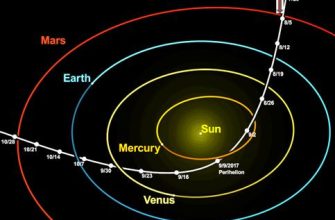
• Аэрокосмическая инженерия: Расчет траекторий ракет, спутников и других летательных аппаратов.
• Компьютерная графика: Моделирование движения объектов в играх и анимации.
• Молекулярная динамика: Изучение поведения атомов и молекул.
• Экономика: Прогнозирование изменений на финансовых рынках.
• Метеорология: Предсказание погоды.

Основные методы численного интегрирования

Существует множество методов численного интегрирования, каждый из которых имеет свои особенности, преимущества и недостатки. Мы рассмотрим наиболее распространенные из них.

Метод Эйлера

Это самый простой и интуитивно понятный метод численного интегрирования. Идея заключается в том, чтобы аппроксимировать значение функции в следующей точке, используя значение функции и ее производной в текущей точке. Формула метода Эйлера выглядит следующим образом:

y_i+1 = y_i + h * f(t_i, y_i)

где:

• y_i+1 – значение функции в следующей точке
• y_i – значение функции в текущей точке
• h – размер шага
• f(t_i, y_i) – значение производной функции в текущей точке

Метод Эйлера прост в реализации, но имеет низкую точность. Ошибка метода накапливается с каждым шагом, что может привести к значительным отклонениям от истинного решения, особенно при больших размерах шага.

Метод Рунге-Кутты

Методы Рунге-Кутты представляют собой семейство методов численного интегрирования, которые обеспечивают более высокую точность, чем метод Эйлера. Эти методы используют несколько промежуточных вычислений производной функции на каждом шаге, чтобы получить более точную аппроксимацию значения функции в следующей точке.

Одним из наиболее популярных методов Рунге-Кутты является метод Рунге-Кутты 4-го порядка (RK4). Формулы для RK4 выглядят следующим образом:

k₁ = f(t_i, y_i)

k₂ = f(t_i + h/2, y_i + h/2 * k₁)

k₃ = f(t_i + h/2, y_i + h/2 * k₂)

k₄ = f(t_i + h, y_i + h * k₃)

y_i+1 = y_i + h/6 * (k₁ + 2 * k₂ + 2 * k₃ + k₄)

Метод RK4 является более точным, чем метод Эйлера, но требует больше вычислительных ресурсов. Он обеспечивает хороший баланс между точностью и вычислительной сложностью и широко используется в различных приложениях.

Метод Верле

Метод Верле является специальным методом численного интегрирования, который часто используется для моделирования динамики частиц. Он обладает хорошими свойствами сохранения энергии и симметрии, что делает его особенно подходящим для моделирования физических систем.

Основная идея метода Верле заключается в том, чтобы использовать информацию о положении частицы в предыдущий момент времени для вычисления ее положения в следующий момент времени. Формула метода Верле выглядит следующим образом:

x_i+1 = 2 * x_i ⎯ x_i-1 + h² * a_i

где:

• x_i+1 – положение частицы в следующий момент времени
• x_i – положение частицы в текущий момент времени
• x_i-1 – положение частицы в предыдущий момент времени
• h – размер шага
• a_i – ускорение частицы в текущий момент времени

Метод Верле не требует явного вычисления скорости частицы, что может быть полезно в некоторых случаях. Однако он может быть менее точным, чем методы Рунге-Кутты, особенно при больших размерах шага.

Выбор метода численного интегрирования

Выбор метода численного интегрирования зависит от конкретной задачи и требований к точности и вычислительной сложности. При выборе метода следует учитывать следующие факторы:

• Точность: Насколько точное решение вам необходимо?
• Вычислительная сложность: Сколько времени и ресурсов вы готовы потратить на вычисления?
• Устойчивость: Насколько устойчив метод к ошибкам округления и другим факторам?
• Свойства сохранения: Важно ли сохранение энергии и других физических величин?

В общем случае, для задач, требующих высокой точности, следует использовать методы Рунге-Кутты высокого порядка. Для задач, где важны свойства сохранения, следует использовать метод Верле или другие специализированные методы.

Для простых задач, где не требуется высокая точность, можно использовать метод Эйлера. Однако следует помнить, что метод Эйлера может быть неустойчивым при больших размерах шага.

Практические советы по численному интегрированию

Вот несколько практических советов, которые помогут вам получить более точные и надежные результаты при численном интегрировании:

1. Выбирайте подходящий размер шага: Слишком большой размер шага может привести к низкой точности и неустойчивости. Слишком маленький размер шага может увеличить время вычислений.
2. Используйте адаптивный размер шага: Адаптивный размер шага позволяет автоматически изменять размер шага в зависимости от поведения решения. Это может значительно повысить точность и эффективность вычислений.
3. Проверяйте сходимость решения: Убедитесь, что решение сходится к определенному значению при уменьшении размера шага. Если решение не сходится, это может указывать на ошибку в коде или на неустойчивость метода.
4. Используйте визуализацию: Визуализация результатов численного интегрирования может помочь вам понять поведение системы и обнаружить ошибки.
5. Сравнивайте результаты с аналитическими решениями: Если возможно, сравнивайте результаты численного интегрирования с аналитическими решениями для простых случаев. Это поможет вам убедиться в правильности вашего кода и оценить точность метода.

Пример: Моделирование движения маятника

Давайте рассмотрим пример моделирования движения маятника с помощью численного интегрирования. Уравнение движения маятника выглядит следующим образом:

θ» + (g/L) * sin(θ) = 0

где:

• θ – угол отклонения маятника от вертикали
• g – ускорение свободного падения
• L – длина маятника

Это дифференциальное уравнение второго порядка, которое можно преобразовать в систему двух дифференциальных уравнений первого порядка:

θ’ = ω

ω’ = -(g/L) * sin(θ)

где ω – угловая скорость маятника.

Теперь мы можем использовать любой из рассмотренных методов численного интегрирования для решения этой системы уравнений. Например, мы можем использовать метод Рунге-Кутты 4-го порядка (RK4).

Реализация этого примера на Python с использованием библиотеки NumPy может выглядеть следующим образом:

import numpy as np
import matplotlib.pyplot as plt

def pendulum_equation(theta, omega, g, L):
"""Уравнение движения маятника."""
dtheta_dt = omega
domega_dt = -(g/L) * np.sin(theta)
return dtheta_dt, domega_dt
def rk4_step(theta, omega, t, dt, g, L):
"""Один шаг метода Рунге-Кутты 4-го порядка."""
k1_theta, k1_omega = pendulum_equation(theta, omega, g, L)
k2_theta, k2_omega = pendulum_equation(theta + dt/2 * k1_theta, omega + dt/2 * k1_omega, g, L)
k3_theta, k3_omega = pendulum_equation(theta + dt/2 * k2_theta, omega + dt/2 * k2_omega, g, L)
k4_theta, k4_omega = pendulum_equation(theta + dt * k3_theta, omega + dt * k3_omega, g, L)
theta_new = theta + dt/6 * (k1_theta + 2k2_theta + 2k3_theta + k4_theta)
omega_new = omega + dt/6 * (k1_omega + 2k2_omega + 2k3_omega + k4_omega)
return theta_new, omega_new

# Параметры маятника
g = 9.81 # Ускорение свободного падения
L = 1.0 # Длина маятника

# Начальные условия
theta_0 = np.pi/4 # Начальный угол
omega_0 = 0.0 # Начальная угловая скорость

# Временной интервал
t_start = 0.0
t_end = 10.0
dt = 0.01

# Инициализация массивов для хранения результатов
time = np.arange(t_start, t_end, dt)
theta = np.zeros_like(time)
omega = np.zeros_like(time)

# Начальные значения
theta[0] = theta_0
omega[0] = omega_0

# Численное интегрирование
for i in range(1, len(time)):
theta[i], omega[i] = rk4_step(theta[i-1], omega[i-1], time[i-1], dt, g, L)

# Построение графика
plt.plot(time, theta)
plt.xlabel("Время (с)")
plt.ylabel("Угол (рад)")
plt.title("Движение маятника (RK4)")
plt.grid(True)
plt.show

Этот код моделирует движение маятника в течение 10 секунд с шагом 0.01 секунды и строит график зависимости угла отклонения маятника от времени.

Численное интегрирование траекторий – это мощный инструмент, который позволяет нам моделировать и предсказывать поведение сложных систем, даже если аналитические решения недоступны. Мы рассмотрели основные методы численного интегрирования, их преимущества и недостатки, а также области применения. Надеемся, что эта статья помогла вам лучше понять принципы численного интегрирования и вдохновила вас на дальнейшие исследования в этой увлекательной области.

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
Численные методы решения ОДУ	Алгоритмы интегрирования траекторий	Метод Эйлера для траекторий	Метод Рунге-Кутты в динамике	Метод Верле для моделирования
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
Применение численного интегрирования	Точность численного интегрирования	Устойчивость численных методов	Моделирование движения тел	Численное интегрирование в Python