Покоряя Космос: Расчет Траекторий с Учетом Гравитационного Влияния

Космос всегда манил человечество своей загадочностью и бескрайними просторами. Мечты о полетах к звездам‚ о колонизации других планет‚ о разгадке тайн Вселенной – все это толкает нас вперед‚ заставляя искать новые пути и решения. Но прежде чем отправиться в это захватывающее путешествие‚ необходимо научиться точно рассчитывать траектории космических аппаратов‚ учитывая все факторы‚ которые могут повлиять на их движение. И одним из самых важных факторов является гравитационное воздействие сторонних тел.

В этой статье мы‚ как опытные исследователи космоса‚ поделимся своим опытом и знаниями о методах расчета траекторий с учетом влияния гравитации других небесных тел. Мы расскажем о сложностях‚ с которыми сталкиваются ученые и инженеры при планировании космических миссий‚ и о том‚ как современные технологии помогают нам преодолевать эти трудности. Приготовьтесь к увлекательному путешествию в мир небесной механики и космической навигации!

Основы небесной механики и гравитационного взаимодействия

Прежде чем погрузиться в сложные алгоритмы и математические модели‚ давайте вспомним основы небесной механики. В центре всего – закон всемирного тяготения‚ открытый Исааком Ньютоном. Он гласит‚ что любое тело с массой притягивает другое тело с массой с силой‚ пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Эта простая формула лежит в основе всех расчетов траекторий.

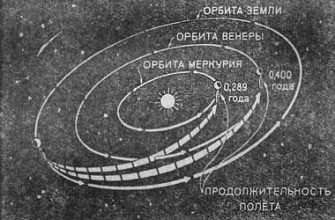
Однако‚ в реальном космосе все гораздо сложнее. На космический аппарат воздействуют не только гравитационное поле Земли (или другого небесного тела‚ вокруг которого он вращается)‚ но и гравитация Солнца‚ Луны‚ других планет и даже крупных астероидов. Учет всех этих факторов – задача нетривиальная‚ требующая применения сложных математических методов и вычислительной техники.

Проблема N тел: вызов для ученых

Задача N тел – это классическая проблема небесной механики‚ которая заключаеться в определении движения N тел‚ взаимодействующих друг с другом посредством гравитации. В общем случае эта задача не имеет аналитического решения‚ то есть решения‚ которое можно выразить в виде формулы. Это означает‚ что для расчета траекторий приходится использовать численные методы‚ которые позволяют получить приближенное решение с заданной точностью.

Чем больше тел учитывается в расчетах‚ тем сложнее становится задача и тем больше вычислительных ресурсов требуется для ее решения. Поэтому ученые и инженеры постоянно ищут новые методы и алгоритмы‚ которые позволяют упростить расчеты и повысить их точность.

Методы расчета траекторий с учетом гравитационного влияния

Существует множество методов расчета траекторий‚ учитывающих гравитационное влияние сторонних тел. Все их можно разделить на несколько основных категорий:

• Аналитические методы: основаны на использовании математических формул и уравнений. Они позволяют получить точное решение в простых случаях‚ например‚ при движении вокруг одного центрального тела.
• Численные методы: используют компьютерные алгоритмы для приближенного решения уравнений движения. Они позволяют учитывать гравитационное влияние множества тел‚ но требуют больших вычислительных ресурсов.
• Гибридные методы: сочетают в себе аналитические и численные методы. Они позволяют получить более точное и быстрое решение‚ чем при использовании только численных методов.

Аналитические методы: простота и точность в простых случаях

Аналитические методы‚ такие как метод Кеплера‚ позволяют точно рассчитывать траектории при движении вокруг одного центрального тела. Они основаны на использовании законов Кеплера‚ которые описывают движение планет вокруг Солнца. Однако‚ эти методы не учитывают гравитационное влияние других тел‚ поэтому их применение ограничено простыми случаями.

Например‚ если мы хотим рассчитать траекторию спутника‚ вращающегося вокруг Земли‚ то можем использовать метод Кеплера‚ пренебрегая гравитационным влиянием Солнца и Луны. В этом случае мы получим достаточно точное решение‚ но только на коротком промежутке времени.

Численные методы: учет множества факторов

Численные методы‚ такие как метод Рунге-Кутты и метод Верле‚ позволяют учитывать гравитационное влияние множества тел. Они основаны на дискретизации времени и аппроксимации уравнений движения. Эти методы позволяют получить приближенное решение с заданной точностью‚ но требуют больших вычислительных ресурсов.

Например‚ если мы хотим рассчитать траекторию космического аппарата‚ летящего к Марсу‚ то нам необходимо учитывать гравитационное влияние Земли‚ Солнца‚ Марса и других планет. В этом случае нам необходимо использовать численные методы‚ чтобы получить достаточно точное решение.

Примеры численных методов:

1. Метод Эйлера
2. Метод Рунге-Кутты (различных порядков точности)
3. Метод Верле
4. Метод Адамса-Башфорта

Гибридные методы: сочетание преимуществ

Гибридные методы сочетают в себе аналитические и численные методы. Они позволяют получить более точное и быстрое решение‚ чем при использовании только численных методов. Например‚ можно использовать аналитический метод для расчета траектории вокруг одного тела‚ а затем использовать численный метод для учета гравитационного влияния других тел.

Этот подход позволяет значительно сократить вычислительные затраты и повысить точность расчетов. Гибридные методы широко используются при планировании сложных космических миссий‚ таких как полеты к дальним планетам и астероидам.

Факторы‚ влияющие на точность расчетов

Точность расчетов траекторий зависит от множества факторов‚ включая:

• Точность определения параметров орбит небесных тел: чем точнее мы знаем параметры орбит Земли‚ Солнца‚ Луны и других планет‚ тем точнее мы можем рассчитать траекторию космического аппарата.
• Точность определения массы небесных тел: чем точнее мы знаем массу Земли‚ Солнца‚ Луны и других планет‚ тем точнее мы можем рассчитать гравитационное влияние этих тел на космический аппарат.
• Точность учета негравитационных сил: на космический аппарат воздействуют не только гравитационные силы‚ но и негравитационные силы‚ такие как сопротивление атмосферы‚ давление солнечного света и тяга двигателей. Учет этих сил также важен для точного расчета траекторий.
• Вычислительная мощность: чем больше вычислительной мощности мы имеем‚ тем более точные и сложные расчеты мы можем проводить.

Повышение точности расчетов траекторий – это постоянный процесс‚ требующий применения новых технологий и методов.

Применение методов расчета траекторий в космических миссиях

Методы расчета траекторий широко используются при планировании и осуществлении космических миссий. Они позволяют:

• Определить оптимальную траекторию полета: методы расчета траекторий позволяют выбрать наиболее экономичную и безопасную траекторию полета к заданной цели.
• Рассчитать необходимое количество топлива: методы расчета траекторий позволяют определить‚ сколько топлива необходимо для выполнения маневров и достижения цели.
• Определить время прибытия к цели: методы расчета траекторий позволяют точно рассчитать время прибытия космического аппарата к заданной цели.
• Скорректировать траекторию в процессе полета: методы расчета траекторий позволяют корректировать траекторию космического аппарата в процессе полета‚ чтобы компенсировать ошибки и неточности.

Без точных расчетов траекторий осуществление космических миссий было бы невозможным.

Примеры успешных миссий‚ основанных на точных расчетах

Многие успешные космические миссии были основаны на точных расчетах траекторий‚ учитывающих гравитационное влияние сторонних тел. Вот несколько примеров:

• Миссия "Вояджер": два космических аппарата "Вояджер" были запущены в 1977 году и совершили облет Юпитера‚ Сатурна‚ Урана и Нептуна. Траектории "Вояджеров" были тщательно рассчитаны с учетом гравитационного влияния этих планет‚ что позволило значительно сократить время полета и увеличить научную отдачу миссии.
• Миссия "Кассини-Гюйгенс": космический аппарат "Кассини" был запущен в 1997 году и достиг Сатурна в 2004 году. "Кассини" исследовал Сатурн и его спутники в течение 13 лет. Траектория "Кассини" была тщательно рассчитана с учетом гравитационного влияния Сатурна и его спутников‚ что позволило выполнить множество научных экспериментов и получить ценные данные.
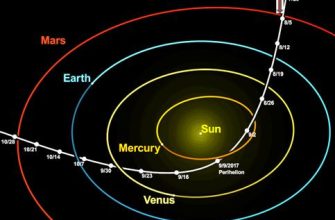
• Миссия "Розетта": космический аппарат "Розетта" был запущен в 2004 году и достиг кометы 67P/Чурюмова-Герасименко в 2014 году. "Розетта" исследовала комету в течение двух лет и сбросила на ее поверхность посадочный модуль "Филы". Траектория "Розетты" была тщательно рассчитана с учетом гравитационного влияния Солнца и кометы‚ что позволило выполнить уникальные научные исследования.

Будущее расчетов траекторий в космосе

Будущее расчетов траекторий в космосе связано с развитием новых технологий и методов‚ таких как:

• Искусственный интеллект и машинное обучение: эти технологии могут быть использованы для разработки более точных и эффективных алгоритмов расчета траекторий.
• Квантовые вычисления: квантовые компьютеры могут позволить решать задачи небесной механики‚ которые сейчас не под силу современным компьютерам.
• Разработка новых датчиков и инструментов для измерения параметров орбит небесных тел: повышение точности измерений позволит повысить точность расчетов траекторий.

В будущем мы сможем планировать и осуществлять еще более сложные и амбициозные космические миссии‚ благодаря развитию методов расчета траекторий.

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
Гравитационное воздействие планет	Численные методы небесной механики	Траектория космического аппарата	Метод Рунге-Кутты в космосе	Моделирование гравитационных полей
Небесная механика для начинающих	Оптимизация траекторий полета	Влияние солнечного давления на траекторию	Расчет траекторий комет	Проблема трех тел решение