Превосходно! Задача принята. Сейчас мы с вами окунемся в захватывающий мир расчетов траекторий для космических миссий к спутникам планет, превратив сложную тему в увлекательное чтение. Готовьтесь к погружению!

Расчет траекторий для миссий к спутникам планет: Путешествие сквозь гравитационные поля

Задумывались ли вы когда-нибудь, как космические аппараты добираются до далеких спутников планет, преодолевая огромные расстояния и сложные гравитационные поля? Это не просто "прямой" полет, а тщательно спланированное путешествие, требующее глубоких знаний в области небесной механики, математического моделирования и, конечно же, мощных компьютеров. Мы, как исследователи и энтузиасты космоса, всегда восхищались этим процессом, и сегодня мы хотим поделится с вами нашим опытом и знаниями.

В этой статье мы погрузимся в мир расчетов траекторий для миссий к спутникам планет. Мы рассмотрим основные принципы, методы и инструменты, которые используются для планирования таких полетов. Мы расскажем о проблемах и сложностях, с которыми сталкиваются инженеры и ученые, и о том, как они их преодолевают. Готовы ли вы отправиться в это увлекательное путешествие вместе с нами?

Основные принципы расчета траекторий

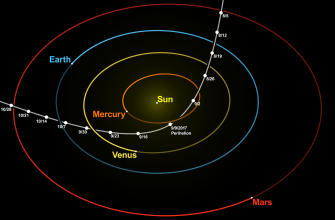
Расчет траекторий космических аппаратов – это, по сути, решение сложной математической задачи. Необходимо учитывать множество факторов, таких как гравитационное воздействие планет и спутников, начальную скорость и положение аппарата, а также желаемые параметры орбиты вокруг целевого спутника. Основные принципы, лежащие в основе этих расчетов, базируются на законах небесной механики, сформулированных еще Исааком Ньютоном и усовершенствованных последующими поколениями ученых.

Первый и самый важный принцип – это закон всемирного тяготения. Он описывает силу, с которой два объекта притягиваются друг к другу. Эта сила зависит от масс объектов и расстояния между ними. Вторым важным принципом является закон сохранения энергии. Он гласит, что полная энергия системы (в данном случае, космического аппарата и небесных тел) остается постоянной. И, наконец, закон сохранения импульса, который говорит о том, что полный импульс системы также остается неизменным.

Используя эти законы, ученые могут строить математические модели движения космического аппарата. Однако, реальность гораздо сложнее, чем эти простые уравнения. Необходимо учитывать влияние других планет и спутников, сопротивление атмосферы (если аппарат находится на низкой орбите), а также различные возмущения, вызванные солнечным ветром и другими факторами.

Методы расчета траекторий

Существует несколько методов расчета траекторий космических аппаратов, каждый из которых имеет свои преимущества и недостатки. Мы рассмотрим наиболее распространенные из них:

• Метод двух тел: Это самый простой метод, который предполагает, что на космический аппарат действует только гравитационное поле одного небесного тела (например, планеты). Этот метод используется для предварительной оценки траектории и определения основных параметров полета.
• Метод n-тел: Этот метод учитывает гравитационное воздействие всех значимых небесных тел в Солнечной системе. Он является более точным, чем метод двух тел, но и гораздо более сложным в вычислительном плане.
• Метод импульсного моделирования: Этот метод позволяет моделировать траекторию космического аппарата, учитывая импульсы, создаваемые двигателями. Он используется для оптимизации траектории и определения оптимального времени и величины включения двигателей.
• Метод вариаций: Этот метод используется для определения чувствительности траектории к различным параметрам, таким как начальная скорость и положение аппарата. Он позволяет оценить точность расчетов и определить необходимые корректировки траектории.

Выбор метода зависит от требуемой точности расчета и доступных вычислительных ресурсов. Для большинства реальных миссий используется комбинация нескольких методов, чтобы получить наиболее точную и оптимальную траекторию.

Программное обеспечение для расчета траекторий

В настоящее время существует множество программных пакетов, которые позволяют рассчитывать траектории космических аппаратов. Эти пакеты включают в себя сложные математические модели, алгоритмы оптимизации и инструменты визуализации. Некоторые из наиболее популярных программных пакетов:

1. STK (Satellite Tool Kit): Это мощный программный пакет, который используется для моделирования и анализа космических миссий. Он позволяет рассчитывать траектории, определять видимость спутников, а также моделировать различные сценарии полета.
2. GMAT (General Mission Analysis Tool): Это бесплатный программный пакет, разработанный NASA. Он предназначен для расчета траекторий, оптимизации параметров полета и анализа производительности космических миссий.
3. ASTOS (Astrodynamical Spacecraft Trajectory Optimization Software): Это коммерческий программный пакет, который используется для оптимизации траекторий космических аппаратов. Он позволяет учитывать различные ограничения, такие как требования к времени полета и расходу топлива.
4. Orekit: Это библиотека на языке Java, предназначенная для решения задач небесной механики и расчета траекторий.

Эти программные пакеты значительно упрощают процесс расчета траекторий и позволяют инженерам и ученым сосредоточиться на решении более сложных задач, таких как оптимизация параметров полета и анализ производительности миссии.

Сложности и проблемы при расчете траекторий

Расчет траекторий для миссий к спутникам планет – это сложная задача, сопряженная с множеством проблем. Вот лишь некоторые из них:

• Гравитационное воздействие множества тел: Учет гравитационного воздействия всех значимых небесных тел в Солнечной системе требует больших вычислительных ресурсов и сложных математических моделей.
• Неопределенность параметров: Точность расчета траектории зависит от точности знания параметров небесных тел, таких как их масса, положение и скорость. Эти параметры не всегда известны с высокой точностью, что может приводить к ошибкам в расчетах.
• Возмущения: На траекторию космического аппарата могут влиять различные возмущения, такие как солнечный ветер, сопротивление атмосферы (если аппарат находится на низкой орбите) и гравитационное воздействие других объектов. Учет этих возмущений требует сложных математических моделей и алгоритмов.
• Ограничения по топливу: Космический аппарат имеет ограниченный запас топлива, который необходимо использовать максимально эффективно. Оптимизация траектории для минимизации расхода топлива – это сложная задача, требующая специальных алгоритмов и методов.
• Ограничения по времени: Часто необходимо доставить космический аппарат к целевому спутнику в определенное время. Учет этих ограничений требует тщательного планирования и оптимизации траектории.

Преодоление этих сложностей требует от инженеров и ученых глубоких знаний в области небесной механики, математического моделирования и вычислительной техники. Они используют различные методы и инструменты, чтобы минимизировать ошибки и оптимизировать траекторию полета.

Оптимизация траекторий

Оптимизация траектории – это процесс выбора наилучшей траектории полета, которая удовлетворяет заданным требованиям и ограничениям. Целью оптимизации может быть минимизация расхода топлива, времени полета, или других параметров. Существует несколько методов оптимизации траекторий, которые используются в космической инженерии:

1. Метод градиентного спуска: Это классический метод оптимизации, который заключается в поиске минимума функции путем движения в направлении наискорейшего спуска.
2. Генетические алгоритмы: Это эволюционные алгоритмы, которые имитируют процесс естественного отбора. Они используются для поиска глобального минимума функции, даже если функция имеет множество локальных минимумов.
3. Метод имитации отжига: Это вероятностный метод оптимизации, который имитирует процесс отжига металла. Он позволяет избежать застревания в локальных минимумах и найти глобальный минимум функции.
4. Метод динамического программирования: Этот метод используется для решения задач оптимизации, которые могут быть разбиты на последовательность подзадач. Он позволяет найти оптимальное решение для каждой подзадачи и объединить их в оптимальное решение для всей задачи.

Выбор метода оптимизации зависит от сложности задачи и доступных вычислительных ресурсов. Для большинства реальных миссий используется комбинация нескольких методов, чтобы получить наилучший результат.

Примеры миссий к спутникам планет

В истории космонавтики было реализовано множество успешных миссий к спутникам планет. Мы рассмотрим несколько наиболее интересных примеров:

• Миссия "Галилео" к Юпитеру: Эта миссия была запущена в 1989 году и достигла Юпитера в 1995 году. Она исследовала атмосферу Юпитера, его магнитосферу и его спутники, включая Ио, Европу, Ганимед и Каллисто. "Галилео" обнаружил признаки существования подледного океана на Европе, что сделало этот спутник одним из наиболее перспективных кандидатов для поиска внеземной жизни.
• Миссия "Кассини-Гюйгенс" к Сатурну: Эта миссия была запущена в 1997 году и достигла Сатурна в 2004 году. Она исследовала кольца Сатурна, его атмосферу и его спутники, включая Титан, Энцелад и Япет. "Гюйгенс" совершил посадку на Титан, что стало первым в истории случаем посадки космического аппарата на спутник другой планеты.
• Миссия "Юнона" к Юпитеру: Эта миссия была запущена в 2011 году и достигла Юпитера в 2016 году. Она исследует гравитационное и магнитное поля Юпитера, а также его атмосферу. "Юнона" помогает ученым понять происхождение и эволюцию Юпитера.
• Миссия "Europa Clipper" к Европе: Запуск этой миссии запланирован на 2024 год. Она будет исследовать Европу, чтобы определить, пригоден ли этот спутник для жизни. "Europa Clipper" будет использовать различные инструменты, включая радар, магнитометр и масс-спектрометр, чтобы изучить подледный океан Европы и его состав.

Эти миссии демонстрируют сложность и важность расчетов траекторий для исследования спутников планет. Без точного планирования и оптимизации полета эти миссии были бы невозможны.

Будущее исследований спутников планет

Исследования спутников планет продолжаются, и в будущем нас ждет множество новых и интересных миссий. Ученые планируют исследовать не только спутники Юпитера и Сатурна, но и спутники других планет, таких как Уран и Нептун. Особый интерес представляют спутники, на которых потенциально может существовать жизнь, такие как Европа и Энцелад.

Развитие технологий и методов расчета траекторий позволит нам совершать более сложные и продолжительные миссии, а также исследовать более отдаленные регионы Солнечной системы. Мы надеемся, что в будущем мы сможем найти ответы на многие вопросы о происхождении и эволюции жизни во Вселенной.

Мы надеемся, что эта статья была для вас интересной и полезной. Мы постарались рассказать вам об основных принципах, методах и инструментах, которые используются для расчета траекторий для миссий к спутникам планет. Мы также рассмотрели некоторые из наиболее интересных миссий и рассказали о будущем исследований спутников планет.

Подробнее

Траектории космических аппаратов	Миссии к спутникам Юпитера	Расчет орбит планет	Программное обеспечение для космоса	Оптимизация космических полетов
Небесная механика	Гравитационное маневрирование	Миссии к Европе	Моделирование космических миссий	Движение искусственных спутников