Прогнозирование будущего: Методы определения ошибки траектории

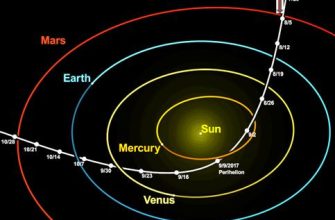
Все мы, в той или иной степени, занимаемся прогнозированием. Будь то планирование отпуска, оценка финансовых рисков или даже просто выбор маршрута до работы, мы постоянно пытаемся предвидеть будущее. Но как же оценить, насколько точны наши прогнозы? Особенно, когда речь идет о сложных системах, таких как траектории движения объектов? В этой статье мы, опираясь на наш опыт, разберем различные методы определения ошибки прогноза траектории, их сильные и слабые стороны, и поделимся практическими советами, которые помогут вам повысить точность ваших предсказаний.

В сущности, прогнозирование траектории – это попытка описать будущее положение объекта в пространстве на основе имеющихся данных о его текущем состоянии и динамике. Это может быть траектория спутника, летящего в космосе, маршрут беспилотного автомобиля или даже движение мяча, брошенного в корзину. Точность прогноза критически важна во многих областях, от навигации и управления воздушным движением до робототехники и компьютерной графики. Именно поэтому так важно уметь оценивать и минимизировать ошибку прогноза.

Что такое ошибка прогноза траектории?

Прежде чем углубляться в методы оценки, давайте четко определим, что мы подразумеваем под ошибкой прогноза траектории. В самом общем виде, это разница между предсказанным положением объекта в определенный момент времени и его фактическим положением. Эта разница может быть выражена в различных единицах измерения – метрах, километрах, градусах (для угловых перемещений) – в зависимости от конкретной задачи.

Важно понимать, что ошибка прогноза – это не просто случайное отклонение. Она может быть систематической, то есть иметь определенную закономерность. Например, наш алгоритм может постоянно недооценивать скорость объекта, что приведет к тому, что предсказанная траектория будет всегда отставать от фактической. Выявление и устранение таких систематических ошибок – ключевой шаг к повышению точности прогнозов.

Источники ошибок прогноза

Ошибки прогноза траектории могут возникать из множества источников. Вот лишь некоторые из них:

• Неточность исходных данных: Наши прогнозы строятся на основе данных о текущем состоянии объекта. Если эти данные неточные (например, из-за ошибок измерения или шума в сенсорах), то и прогноз будет неточным.
• Несовершенство модели: Мы используем математические модели для описания динамики объекта. Эти модели – упрощение реальности, и они неизбежно содержат погрешности. Например, мы можем пренебречь некоторыми силами, действующими на объект, или использовать неточные значения параметров модели.
• Вычислительные ошибки: Даже если наша модель идеальна, а исходные данные точны, мы все равно можем столкнуться с ошибками из-за ограничений вычислительной техники. Например, при численном решении дифференциальных уравнений неизбежно возникают ошибки округления.
• Внешние факторы: На траекторию объекта могут влиять внешние факторы, которые трудно предсказать. Например, на движение воздушного судна могут влиять порывы ветра, а на движение автомобиля – действия других участников дорожного движения.

Методы определения ошибки прогноза траектории

Существует множество методов определения ошибки прогноза траектории, каждый из которых имеет свои преимущества и недостатки. Мы рассмотрим наиболее распространенные и эффективные из них.

Статистические методы

Статистические методы основаны на анализе большого количества прогнозов и сравнении их с фактическими траекториями. Они позволяют оценить общую точность прогнозов и выявить систематические ошибки.

Среднеквадратичная ошибка (MSE)

Среднеквадратичная ошибка (MSE) – один из самых популярных показателей точности прогнозов. Она вычисляется как среднее арифметическое квадратов разностей между предсказанными и фактическими значениями. Чем меньше значение MSE, тем точнее прогнозы.

Формула MSE:

MSE = (1/n) * Σ(y_i ― ŷ_i)²

где:

• n – количество прогнозов
• y_i – фактическое значение
• ŷ_i – предсказанное значение

Средняя абсолютная ошибка (MAE)

Средняя абсолютная ошибка (MAE) – еще один распространенный показатель точности прогнозов. Она вычисляется как среднее арифметическое абсолютных значений разностей между предсказанными и фактическими значениями. MAE менее чувствительна к выбросам, чем MSE.

Формула MAE:

MAE = (1/n) * Σ|y_i ‒ ŷ_i|

где:

• n – количество прогнозов
• y_i – фактическое значение
• ŷ_i – предсказанное значение

Корень из среднеквадратичной ошибки (RMSE)

Корень из среднеквадратичной ошибки (RMSE) – это просто квадратный корень из MSE. Он имеет ту же размерность, что и фактические значения, что облегчает интерпретацию результатов.

Формула RMSE:

RMSE = √(MSE)

Коэффициент детерминации (R²)

Коэффициент детерминации (R²) – показатель, который характеризует, насколько хорошо наша модель объясняет дисперсию данных. Он принимает значения от 0 до 1, где 1 означает, что модель идеально объясняет данные, а 0 – что модель не лучше, чем простое среднее значение.

Формула R²:

R² = 1 ‒ (Σ(y_i ‒ ŷ_i)² / Σ(y_i ‒ ȳ)²)

где:

• y_i – фактическое значение
• ŷ_i – предсказанное значение
• ȳ – среднее значение фактических значений

Методы, основанные на анализе остатков

Анализ остатков – это метод, который позволяет выявить систематические ошибки в прогнозах. Остатки – это разности между фактическими и предсказанными значениями. Если остатки распределены случайным образом, то это говорит о том, что наша модель хорошо описывает данные. Если же в остатках наблюдается какая-то закономерность, то это указывает на наличие систематической ошибки.

Например, если остатки положительны в начале траектории и отрицательны в конце, то это может говорить о том, что наша модель недооценивает скорость объекта. Для выявления закономерностей в остатках можно использовать различные графические методы, такие как графики рассеяния, гистограммы и автокорреляционные функции.

Методы перекрестной проверки

Методы перекрестной проверки позволяют оценить, насколько хорошо наша модель обобщает данные, то есть насколько хорошо она будет работать на новых, ранее не виденных данных. Суть этих методов заключается в том, что мы разбиваем имеющиеся данные на несколько частей, обучаем модель на одной части данных и проверяем ее на другой части. Этот процесс повторяется несколько раз, и в итоге мы получаем оценку точности модели на новых данных.

Наиболее распространенные методы перекрестной проверки:

• k-блочная перекрестная проверка: Данные разбиваются на k блоков, и модель обучается на k-1 блоках и проверяется на оставшемся блоке. Этот процесс повторяется k раз, каждый раз с другим блоком в качестве проверочного.
• Перекрестная проверка с исключением одного объекта: Модель обучается на всех данных, кроме одного объекта, и проверяется на этом объекте. Этот процесс повторяется для каждого объекта в наборе данных.

Практические советы по повышению точности прогнозов

Оценка ошибки прогноза – это только первый шаг. Важно также предпринимать шаги по повышению точности прогнозов. Вот несколько практических советов, основанных на нашем опыте:

1. Собирайте качественные данные: Точность прогнозов напрямую зависит от качества исходных данных. Используйте надежные сенсоры, калибруйте их регулярно и очищайте данные от шума и выбросов.
2. Выбирайте подходящую модель: Не все модели одинаково хорошо подходят для решения конкретной задачи. Экспериментируйте с различными моделями и выбирайте ту, которая обеспечивает наилучшую точность прогнозов.
3. Тщательно настраивайте параметры модели: Параметры модели могут существенно влиять на точность прогнозов. Используйте методы оптимизации для поиска оптимальных значений параметров.
4. Учитывайте внешние факторы: По возможности учитывайте внешние факторы, которые могут влиять на траекторию объекта. Например, для прогнозирования траектории воздушного судна учитывайте скорость и направление ветра.
5. Используйте ансамблевые методы: Ансамблевые методы объединяют несколько моделей для получения более точного прогноза. Например, можно обучить несколько различных моделей и усреднить их прогнозы.
6. Постоянно отслеживайте и анализируйте ошибки: Регулярно отслеживайте и анализируйте ошибки прогнозов. Это позволит вам выявить слабые места вашей модели и принять меры по их устранению.

Пример использования: Прогнозирование траектории дрона

Давайте рассмотрим пример использования описанных методов для прогнозирования траектории дрона. Предположим, мы хотим разработать систему, которая могла бы предсказывать, куда полетит дрон в ближайшие несколько секунд, чтобы избежать столкновений с препятствиями.

В качестве исходных данных мы используем показания GPS-сенсора, акселерометра и гироскопа, установленных на дроне. Для моделирования динамики дрона мы используем модель Ньютона, учитывающую силы тяги, сопротивления воздуха и гравитации.

Для оценки точности прогнозов мы используем следующие показатели:

• MSE для координат X, Y и Z
• RMSE для скорости
• R² для ускорения

Мы также анализируем остатки, чтобы выявить систематические ошибки. Например, мы можем обнаружить, что наша модель недооценивает влияние ветра на траекторию дрона. В этом случае мы можем добавить в модель дополнительный член, учитывающий силу ветра.

Для повышения точности прогнозов мы используем фильтр Калмана, который позволяет объединить показания сенсоров и модель динамики для получения более точной оценки состояния дрона. Мы также используем ансамблевый метод, объединяющий прогнозы нескольких моделей, обученных на различных наборах данных.

Прогнозирование траектории – сложная задача, требующая комплексного подхода. Не существует универсального метода, который бы подходил для всех случаев. Выбор конкретного метода зависит от конкретной задачи, доступных данных и вычислительных ресурсов. Однако, используя описанные в этой статье методы и советы, вы сможете значительно повысить точность ваших прогнозов и решать сложные задачи в различных областях. Мы надеемся, что наш опыт будет вам полезен.

Подробнее

Оценка точности прогноза траектории	Методы анализа ошибок прогнозирования	Статистические показатели точности	Алгоритмы прогнозирования траекторий	Перекрестная проверка прогнозов
Оптимизация параметров модели траектории	Источники ошибок в прогнозировании	Применение фильтра Калмана	Анализ остатков прогноза	Повышение точности траектории