Путешествие к Сатурну: Математика и Магия Расчета Траекторий Спутников

Когда мы смотрим на ночное небо, усыпанное звездами, Сатурн с его величественными кольцами кажется чем-то далеким и недостижимым. Но за каждым космическим аппаратом, бороздящим просторы Вселенной, стоит кропотливая работа ученых и инженеров, рассчитывающих траектории с невероятной точностью. Сегодня мы погрузимся в мир этих расчетов, приоткроем завесу тайны и посмотрим, как математика помогает нам исследовать одну из самых красивых планет нашей Солнечной системы.

Представьте себе, что мы – команда, которой поручено отправить спутник на орбиту Сатурна. Задача непростая, но безумно интересная. Нам предстоит учесть множество факторов, от гравитационного влияния других планет до солнечного давления. И все это для того, чтобы наш аппарат достиг цели и успешно выполнял свою миссию.

Зачем вообще нужны спутники у Сатурна?

Прежде чем углубляться в математические дебри, давайте разберемся, зачем нам вообще отправлять спутники к Сатурну. Ответ прост: для науки! Спутники, вращающиеся вокруг Сатурна, предоставляют уникальную возможность изучать планету, ее кольца и многочисленные спутники. Они могут собирать данные о составе атмосферы, магнитном поле, структуре колец и даже искать признаки жизни на таких спутниках, как Энцелад и Титан.

• Изучение атмосферы: Спутники могут измерять температуру, давление, состав и движение атмосферы Сатурна, помогая нам понять процессы, происходящие в ней.
• Исследование колец: Кольца Сатурна – это сложная и динамичная система, состоящая из миллиардов ледяных частиц. Спутники могут изучать их структуру, состав и взаимодействие между частицами.
• Поиск жизни: Энцелад и Титан – два спутника Сатурна, на которых существуют условия, потенциально подходящие для жизни. Спутники могут искать органические молекулы и другие признаки жизни на этих телах.

Основы небесной механики: Что нужно знать?

Расчет траекторий космических аппаратов – это область небесной механики, которая, в свою очередь, является разделом астрономии, изучающим движение небесных тел под действием гравитационных сил. Для успешного планирования миссии к Сатурну нам необходимо понимать несколько ключевых концепций.

Законы Кеплера

Иоганн Кеплер, живший в XVII веке, сформулировал три закона, описывающих движение планет вокруг Солнца. Эти законы являются основой для понимания движения любого тела под действием гравитации, в т.ч. и спутников вокруг Сатурна.

1. Первый закон: Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
2. Второй закон: Радиус-вектор, соединяющий планету и Солнце, заметает равные площади за равные промежутки времени. Это означает, что планета движется быстрее, когда находится ближе к Солнцу, и медленнее, когда находится дальше от него.
3. Третий закон: Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Этот закон позволяет нам рассчитать период обращения спутника вокруг Сатурна, зная размер его орбиты.

Закон всемирного тяготения Ньютона

Исаак Ньютон, современник Кеплера, сформулировал закон всемирного тяготения, который объясняет, почему планеты движутся именно так, как описано в законах Кеплера. Согласно этому закону, сила притяжения между двумя телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.

Этот закон позволяет нам рассчитать силу, с которой Сатурн притягивает наш спутник, и, следовательно, определить, как он будет двигаться.

Проблема многих тел

В идеальном мире мы могли бы рассматривать движение спутника вокруг Сатурна как задачу двух тел: спутника и Сатурна. Однако в реальности на спутник влияют гравитационные силы и других тел: Солнца, других планет, спутников Сатурна. Это приводит к так называемой "проблеме многих тел", которая не имеет точного аналитического решения.

Для решения проблемы многих тел используются численные методы, которые позволяют нам с высокой точностью моделировать движение спутника под действием гравитационных сил всех тел Солнечной системы.

Инструменты и методы расчета траекторий

Теперь, когда мы понимаем основы небесной механики, давайте рассмотрим, какие инструменты и методы мы можем использовать для расчета траекторий спутников.

Численное интегрирование

Численное интегрирование – это метод, который позволяет нам приближенно решать дифференциальные уравнения, описывающие движение спутника. Суть метода заключается в том, что мы разбиваем время на небольшие интервалы и на каждом интервале вычисляем изменение положения и скорости спутника под действием гравитационных сил.

Существует множество различных алгоритмов численного интегрирования, таких как метод Эйлера, метод Рунге-Кутты и метод Верле. Выбор конкретного алгоритма зависит от требуемой точности и вычислительной сложности.

Программное обеспечение для моделирования траекторий

Для расчета траекторий космических аппаратов используются специализированные программные пакеты, такие как STK (Satellite Tool Kit), GMAT (General Mission Analysis Tool) и Orekit. Эти пакеты содержат в себе различные модели гравитационного поля, алгоритмы численного интегрирования и инструменты визуализации, которые позволяют нам моделировать движение спутника с высокой точностью.

Мы, как команда, должны уметь пользоваться этими инструментами, чтобы эффективно планировать и корректировать траекторию нашего спутника.

Факторы, влияющие на траекторию

Как мы уже говорили, на траекторию спутника влияет множество факторов, помимо гравитационного поля Сатурна. Давайте рассмотрим некоторые из них.

Гравитационное влияние других планет

Солнце и другие планеты Солнечной системы оказывают гравитационное влияние на спутник, которое может существенно изменить его траекторию. Особенно важно учитывать влияние Юпитера, самой массивной планеты Солнечной системы.

Солнечное давление

Солнечный свет оказывает небольшое, но постоянное давление на спутник, которое может со временем изменить его орбиту. Особенно сильно солнечное давление влияет на спутники с большой площадью поверхности и малой массой.

Атмосфера Сатурна

Хотя атмосфера Сатурна гораздо менее плотная, чем атмосфера Земли, она все же оказывает сопротивление движению спутника, особенно на низких орбитах. Это приводит к постепенному снижению высоты орбиты и, в конечном итоге, к сгоранию спутника в атмосфере.

Неидеальность гравитационного поля Сатурна

Гравитационное поле Сатурна не является идеально сферическим. Оно имеет небольшие отклонения от сферической формы, которые вызваны неоднородным распределением массы внутри планеты. Эти отклонения могут вызывать возмущения в орбите спутника, которые необходимо учитывать при расчете траектории.

Коррекция траектории: Как оставатся на курсе?

Несмотря на все наши усилия по точному расчету траектории, в реальности всегда возникают отклонения от запланированного курса. Это может быть вызвано неточностями в наших моделях, ошибками в измерениях или непредвиденными событиями, такими как столкновения с микрометеоритами.

Для того чтобы наш спутник оставался на заданной орбите, нам необходимо регулярно корректировать его траекторию с помощью небольших импульсов двигателей. Частота и величина этих импульсов зависят от величины отклонений и требуемой точности поддержания орбиты.

Методы коррекции траектории

• Импульсная коррекция: Этот метод заключается в том, что мы включаем двигатели спутника на короткое время, чтобы изменить его скорость и, следовательно, его траекторию.
• Непрерывная коррекция: Этот метод заключается в том, что мы постоянно включаем двигатели спутника на небольшую мощность, чтобы компенсировать влияние возмущающих факторов.

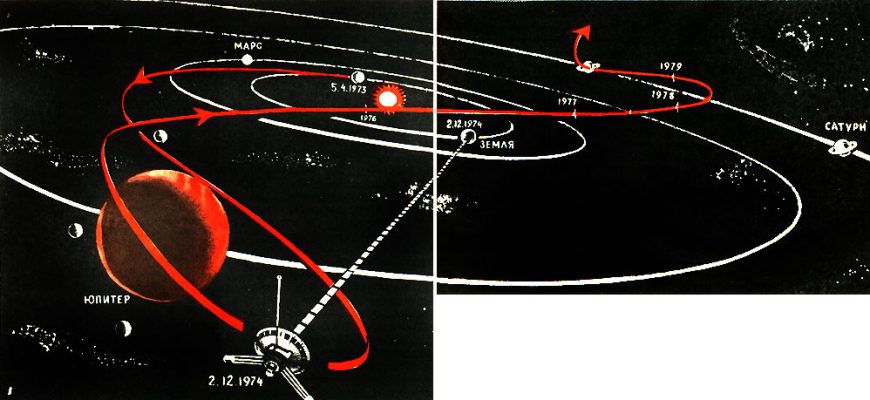
Пример: Миссия Cassini-Huygens

Одним из самых ярких примеров успешной миссии к Сатурну является миссия Cassini-Huygens. Космический аппарат Cassini был запущен в 1997 году и достиг Сатурна в 2004 году. В течение 13 лет он изучал планету, ее кольца и спутники, собрав огромное количество ценных данных.

Одной из самых сложных задач миссии Cassini-Huygens была посадка зонда Huygens на поверхность Титана, самого большого спутника Сатурна. Эта задача потребовала очень точного расчета траектории и системы наведения, чтобы зонд успешно достиг поверхности Титана.

Миссия Cassini-Huygens стала настоящим триумфом науки и техники и показала, что мы способны достигать самых далеких и сложных целей в космосе.

Будущее исследований Сатурна

Хотя миссия Cassini-Huygens завершилась в 2017 году, исследования Сатурна продолжаются. Ученые анализируют данные, собранные Cassini, и разрабатывают новые миссии, которые позволят нам еще глубже изучить эту удивительную планету.

В будущем мы, возможно, отправим новые спутники к Сатурну, которые будут искать признаки жизни на Энцеладе и Титане, изучать структуру колец с еще большей детализацией и исследовать магнитное поле планеты.

Путешествие к Сатурну – это не только научный вызов, но и захватывающее приключение, которое вдохновляет нас на новые открытия и достижения.

Надеемся, что это путешествие в мир расчета траекторий спутников Сатурна было для вас интересным и познавательным. Мы увидели, что за каждым космическим аппаратом стоит кропотливая работа ученых и инженеров, которые с помощью математики и передовых технологий помогают нам исследовать Вселенную.

Подробнее

Траектории спутников	Орбиты Сатурна	Небесная механика	Миссия Cassini	Спутники Сатурна
Расчет орбит	Программное обеспечение для траекторий	Гравитационное поле Сатурна	Коррекция траектории	Законы Кеплера