Путешествие за горизонт: Методы расчета траекторий с учетом гравитационных бурь

Мы, люди, всегда стремились к звездам․ И чтобы наши корабли бороздили космические просторы, нам необходимо понимать и учитывать все силы, действующие на них․ Это задача не из легких, особенно когда речь заходит о влиянии сторонних тел на траекторию полета․ Представьте себе: ваш космический аппарат летит к Марсу, и вдруг, пролетая мимо Юпитера, его траектория начинает изменяться под воздействием гравитации гиганта․ Как предсказать это изменение? Как скорректировать курс, чтобы достичь цели? Именно об этом, о методах расчета траекторий с учетом "гравитационных бурь", мы и поговорим сегодня․

В этой статье мы погрузимся в мир небесной механики, рассмотрим различные подходы к моделированию гравитационного взаимодействия множества тел, и поделимся своим опытом в этой увлекательной области․ Готовьтесь к захватывающему путешествию в мир цифр, формул и космических горизонтов!

Ньютоновская механика: Основа основ

В основе расчета траекторий лежит, конечно же, закон всемирного тяготения Ньютона․ Он описывает силу притяжения между двумя телами, зависящую от их масс и расстояния между ними․ Эта сила, казалось бы, простая, но именно она управляет движением планет, звезд и галактик․ Мы используем этот закон для расчета силы, действующей на космический аппарат со стороны каждого небесного тела, а затем, применяя второй закон Ньютона (F=ma), определяем ускорение аппарата․ Зная ускорение, мы можем вычислить изменение скорости и положения аппарата с течением времени․

Однако, в реальности все гораздо сложнее․ В космосе одновременно действуют силы притяжения от Солнца, планет, лун, астероидов… Задача становится многотельной, и точное аналитическое решение для нее, как правило, невозможно․ Поэтому нам приходится прибегать к численным методам․

Численные методы: Шаг за шагом к цели

Численные методы позволяют нам приближенно решать уравнения движения, разбивая время на маленькие шаги․ На каждом шаге мы рассчитываем силу, действующую на аппарат, определяем его ускорение, и вычисляем изменение скорости и положения․ Повторяя эту процедуру много раз, мы получаем приближенную траекторию полета․ Существует множество численных методов, отличающихся точностью и вычислительной сложностью․ Мы часто используем методы Рунге-Кутты различных порядков, которые обеспечивают хороший баланс между этими двумя параметрами․

Важно отметить, что точность численного метода напрямую зависит от размера шага по времени․ Чем меньше шаг, тем точнее результат, но тем больше времени требуется для расчета․ Поэтому выбор оптимального шага является важной задачей, требующей компромисса․

Проблема трех тел: Вечный вызов

Даже в случае всего трех тел (например, Солнце, Земля и космический аппарат) задача становится чрезвычайно сложной․ В общем случае, у нее не существует аналитического решения․ Это означает, что мы не можем выразить траекторию аппарата в виде простой формулы․ Вместо этого, нам приходится использовать численные методы, и даже они не всегда гарантируют точное предсказание траектории на длительных промежутках времени․ Небольшие ошибки в начальных условиях или в расчетах могут со временем накапливаться и приводить к существенным отклонениям от реальной траектории․

Именно поэтому так важна точность измерений и расчетов, а также постоянная коррекция траектории во время полета․

Метод эфемерид: Использование готовых данных

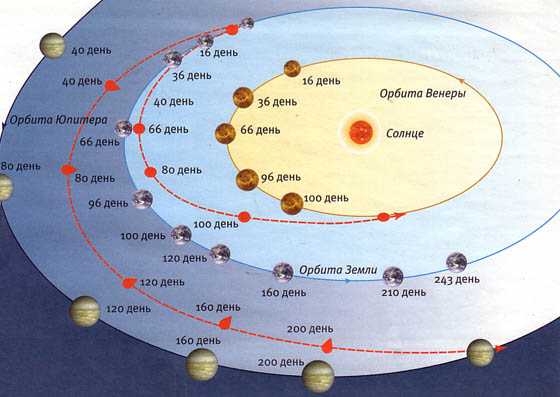
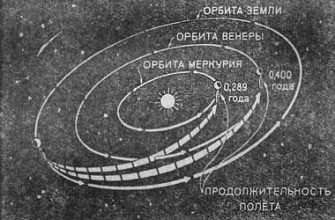
Вместо того, чтобы каждый раз рассчитывать положение небесных тел с нуля, мы можем использовать готовые данные – эфемериды․ Эфемериды – это таблицы, содержащие координаты планет, лун и других объектов в Солнечной системе на различные моменты времени․ Эти данные получаются на основе многолетних наблюдений и тщательных расчетов․ Использование эфемерид позволяет нам значительно ускорить процесс расчета траекторий, особенно при моделировании длительных полетов․

Существуют различные источники эфемерид, такие как NASA’s Jet Propulsion Laboratory (JPL) и International Astronomical Union (IAU)․ Мы выбираем эфемериды в зависимости от требуемой точности и временного интервала․

Гравитационные маневры: Искусство управления гравитацией

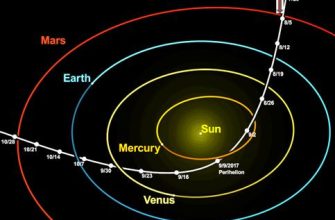
Гравитационный маневр – это использование гравитационного поля планеты для изменения скорости и направления полета космического аппарата․ Пролетая вблизи планеты, аппарат под действием ее гравитации разгоняется или тормозится, и меняет свою траекторию; Гравитационные маневры позволяют значительно экономить топливо, что особенно важно при дальних космических перелетах․ Мы часто используем гравитационные маневры для достижения отдаленных планет или для выхода на определенную орбиту․

Расчет гравитационного маневра – это сложная задача, требующая точного знания траектории аппарата и положения планеты․ Небольшая ошибка в расчетах может привести к тому, что аппарат пролетит мимо планеты или даже столкнется с ней․ Поэтому мы используем специальные алгоритмы оптимизации, которые позволяют найти оптимальную траекторию маневра․

Коррекция траектории: Неизбежная необходимость

Как бы точно мы ни рассчитывали траекторию, в реальности всегда возникают отклонения․ Это связано с различными факторами, такими как неточности в определении параметров аппарата, ошибки в эфемеридах, влияние солнечного ветра и другие непредсказуемые воздействия․ Поэтому во время полета необходимо постоянно отслеживать положение аппарата и корректировать его траекторию с помощью двигателей․ Коррекция траектории – это непрерывный процесс, требующий постоянного внимания и точных расчетов․

Мы используем различные методы коррекции траектории, в зависимости от величины отклонения и доступного запаса топлива․ В некоторых случаях достаточно небольших импульсов двигателей, а в других – требуються более значительные маневры․

Программное обеспечение: Наши инструменты

Для расчета траекторий и моделирования гравитационного взаимодействия мы используем специализированное программное обеспечение․ Существует множество программ, как коммерческих, так и бесплатных, предназначенных для решения задач небесной механики; Мы предпочитаем использовать собственные разработки, основанные на библиотеках численного анализа и визуализации данных․ Это позволяет нам гибко настраивать программное обеспечение под наши конкретные задачи и получать максимальную производительность․

Одним из ключевых компонентов нашего программного обеспечения является модуль визуализации, который позволяет нам отображать траектории полета в трехмерном пространстве, а также визуализировать различные параметры, такие как скорость, ускорение и расстояние до небесных тел․ Визуализация помогает нам лучше понимать процессы, происходящие во время полета, и находить оптимальные решения․

Будущее: Новые горизонты

Расчет траекторий с учетом влияния сторонних тел – это постоянно развивающаяся область․ С развитием технологий появляются новые методы и алгоритмы, позволяющие решать все более сложные задачи․ Мы активно следим за новыми разработками и стараемся внедрять их в нашу работу․ В будущем мы планируем разработать более точные и эффективные методы расчета траекторий, которые позволят нам отправлять космические аппараты к самым отдаленным уголкам Вселенной․

Одним из перспективных направлений является использование искусственного интеллекта для оптимизации траекторий и автоматической коррекции курса․ Мы верим, что искусственный интеллект поможет нам значительно повысить эффективность и надежность космических полетов․

Подробнее

Гравитационное взаимодействие тел	Численное моделирование траекторий	Эфемериды планет	Гравитационные маневры	Коррекция траектории КА
Проблема трех тел решение	Точность расчета траекторий	Методы Рунге-Кутты	Оптимизация траекторий полета	Влияние солнечного ветра на КА