Расчет траекторий для миссий к спутникам планет: От теории к практике межпланетных путешествий

Мечта о покорении космоса всегда будоражила умы человечества. И если путешествия к планетам кажутся нам чем-то уже относительно достижимым‚ то миссии к их спутникам – это следующий‚ еще более сложный и захватывающий этап. Мы‚ как энтузиасты космонавтики‚ всегда задавались вопросом: как же рассчитываются траектории этих сложнейших межпланетных перелетов? Какие факторы необходимо учитывать‚ чтобы космический аппарат достиг своей цели – маленькой луны‚ вращающейся вокруг далекого гиганта?

В этой статье мы погрузимся в увлекательный мир расчетов траекторий для миссий к спутникам планет. Мы рассмотрим основные принципы‚ математические модели и практические аспекты‚ которые позволяют ученым и инженерам планировать эти невероятные путешествия. Приготовьтесь к путешествию в мир небесной механики‚ где гравитация‚ скорость и время сплетаются в сложный‚ но прекрасный танец.

Основы небесной механики и гравитации

Прежде чем говорить о сложных траекториях‚ необходимо вспомнить основы небесной механики. Все начинается с гравитации – силы‚ которая управляет движением небесных тел. Закон всемирного тяготения Ньютона‚ хотя и является упрощением‚ все еще служит основой для большинства расчетов. Он описывает силу притяжения между двумя телами‚ пропорциональную их массам и обратно пропорциональную квадрату расстояния между ними.

Однако‚ в реальной космической миссии все гораздо сложнее. Космический аппарат подвергается воздействию гравитации не только планеты и ее спутника‚ но и Солнца‚ других планет‚ и даже собственной конструкции (хоть и незначительно). Учет всех этих факторов требует использования более сложных моделей‚ основанных на Общей теории относительности Эйнштейна и численных методах.

Проблема трех тел и ее решения

Проблема трех тел – это классическая задача небесной механики‚ которая заключается в определении движения трех тел‚ взаимодействующих друг с другом посредством гравитации. В отличие от проблемы двух тел‚ для которой существует аналитическое решение‚ проблема трех тел в общем случае не имеет точного решения. Это означает‚ что для расчета траекторий космических аппаратов приходится использовать приближенные методы и численные симуляции.

Существуют различные подходы к решению проблемы трех тел‚ включая:

• Метод последовательных приближений: Итеративный процесс‚ в котором на каждом шаге уточняется траектория аппарата.
• Метод ограниченной задачи трех тел: Упрощение‚ при котором масса одного из тел считается пренебрежимо малой.
• Численное интегрирование: Прямое решение уравнений движения с использованием компьютеров.

Выбор оптимальной траектории: Энергия и время

После того‚ как мы разобрались с основами небесной механики‚ необходимо выбрать оптимальную траекторию для миссии. "Оптимальная" в данном случае означает траекторию‚ которая минимизирует затраты энергии и времени‚ необходимые для достижения цели. Важными параметрами‚ которые необходимо учитывать‚ являются:

• ΔV (дельта-V): Общее изменение скорости‚ необходимое для выполнения маневров.
• Время полета: Продолжительность миссии.
• Ограничения по оборудованию: Возможности двигателей‚ систем навигации и связи.
• Безопасность: Минимизация рисков столкновений с другими объектами.

Гравитационные маневры

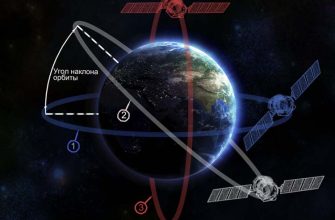
Одним из эффективных способов экономии энергии является использование гравитационных маневров. Суть этого метода заключается в использовании гравитационного поля планеты или спутника для изменения скорости и направления движения космического аппарата. Гравитационные маневры позволяют значительно сократить потребление топлива‚ но требуют точного планирования и навигации.

Представьте себе бильярдный шар (космический аппарат)‚ который‚ пролетая мимо другого шара (планеты)‚ меняет свою траекторию. Правильно рассчитав угол и скорость подлета‚ можно "украсть" энергию у планеты и разогнаться до нужной скорости.

Траектории Хомана и биэллиптические траектории

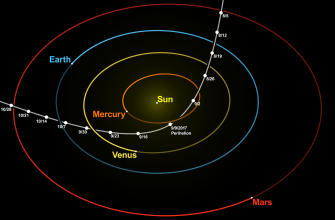
Траектория Хомана – это классическая траектория перелета между двумя копланарными круговыми орбитами. Она представляет собой эллипс‚ касающийся обеих орбит. Траектория Хомана является наиболее энергоэффективной для перелетов между орбитами‚ но она может быть не самой быстрой.

Биэллиптическая траектория – это альтернативный вариант‚ который может быть быстрее траектории Хомана‚ но требует большего ΔV. Биэллиптическая траектория состоит из двух полуэллипсов‚ и позволяет "перепрыгнуть" на более высокую орбиту‚ а затем спуститься на целевую.

Программное обеспечение для расчета траекторий

Расчет траекторий космических аппаратов – это сложная задача‚ требующая использования специализированного программного обеспечения. Существуют различные инструменты‚ которые позволяют ученым и инженерам моделировать движение космических аппаратов‚ оптимизировать траектории и учитывать различные факторы‚ влияющие на полет. Некоторые из наиболее популярных программных пакетов включают:

• STK (Systems Tool Kit): Коммерческий программный пакет для моделирования космических миссий.
• GMAT (General Mission Analysis Tool): Бесплатный программный пакет‚ разрабатываемый NASA;
• Orekit: Бесплатная библиотека для космической динамики на языке Java.

Эти инструменты позволяют моделировать гравитационные поля‚ выполнять численные расчеты траекторий‚ оптимизировать маневры и визуализировать результаты. Они являются незаменимыми помощниками в планировании и реализации космических миссий;

Учет возмущений и неидеальностей

В реальном мире расчеты траекторий усложняются из-за различных возмущений и неидеальностей. К ним относятся:

• Несферичность планет: Планеты не являются идеальными сферами‚ что приводит к отклонениям от закона всемирного тяготения Ньютона.
• Атмосферное сопротивление: Влияет на траекторию аппаратов‚ находящихся на низких орбитах.
• Солнечное давление: Давление солнечного света может оказывать значительное влияние на траекторию легких аппаратов.
• Неточности в определении параметров орбит: Неточности в определении положения и скорости небесных тел могут приводить к ошибкам в расчетах траекторий.

Для учета этих возмущений необходимо использовать более сложные модели и методы коррекции траектории во время полета.

Практические примеры миссий к спутникам планет

Рассмотрим несколько примеров реальных миссий к спутникам планет‚ чтобы увидеть‚ как теория применяется на практике:

• Миссия "Галилео" к Юпитеру и его спутникам: Эта миссия использовала серию гравитационных маневров для исследования Юпитера и его крупнейших спутников‚ включая Ио‚ Европу‚ Ганимед и Каллисто.
• Миссия "Кассини-Гюйгенс" к Сатурну и Титану: "Кассини" провела много лет на орбите Сатурна‚ изучая планету и ее кольца. Аппарат "Гюйгенс" был успешно спущен на Титан‚ крупнейший спутник Сатурна.
• Миссия "Юнона" к Юпитеру: "Юнона" использует высокоэллиптическую полярную орбиту для изучения гравитационного и магнитного полей Юпитера.

Эти миссии демонстрируют сложность и разнообразие задач‚ которые необходимо решать при планировании и реализации космических миссий к спутникам планет.

Будущее миссий к спутникам планет

В будущем нас ждет еще больше захватывающих миссий к спутникам планет. Ученые планируют исследовать подледные океаны Европы и Энцелада в поисках жизни‚ а также изучать геологию и атмосферу Титана. Новые технологии‚ такие как ионные двигатели и автономные системы навигации‚ позволят нам достигать более далеких и сложных целей.

Мы уверены‚ что в ближайшие десятилетия нас ждет множество открытий и прорывов в области исследования спутников планет. Эти миссии не только расширят наши знания о Солнечной системе‚ но и помогут нам лучше понять место человечества во Вселенной.

Мы‚ как энтузиасты космонавтики‚ с нетерпением ждем новых миссий и открытий‚ которые они принесут. Путешествия к спутникам планет – это не просто научный интерес‚ это шаг к покорению новых миров и расширению границ человеческого познания.

Подробнее

Траектории космических аппаратов	Небесная механика	Гравитационные маневры	Миссии к спутникам	Расчет орбит
Проблема трех тел	Космическая навигация	Программное обеспечение для космоса	Энергоэффективные траектории	Исследование спутников планет