Расчет траекторий для спутников на наклонных орбитах: Наш опыт и секреты

Приветствуем вас, уважаемые читатели! Сегодня мы погрузимся в захватывающий мир космонавтики и поделимся нашим личным опытом в расчете траекторий для спутников, вращающихся на наклонных орбитах. Это сложная, но невероятно увлекательная задача, требующая глубоких знаний в математике, физике и программировании. Мы расскажем о трудностях, с которыми сталкивались, и о решениях, которые находили, чтобы вы могли избежать наших ошибок и быстрее достичь успеха в этой области.

В этой статье мы не просто поделимся теоретическими знаниями, а предоставим конкретные примеры и практические советы, основанные на нашем опыте. Мы уверены, что эта информация будет полезна как начинающим специалистам, так и опытным инженерам, работающим в космической отрасли.

Что такое наклонная орбита и почему она важна?

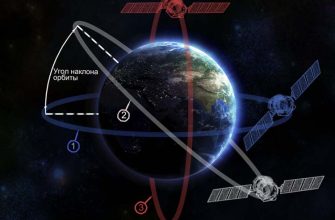
Прежде чем углубляться в детали расчета траекторий, давайте разберемся, что же такое наклонная орбита. Наклонная орбита – это орбита спутника, плоскость которой не совпадает с плоскостью экватора Земли. Угол между плоскостью орбиты и плоскостью экватора называется наклонением орбиты. Наклонные орбиты играют ключевую роль в различных космических миссиях, включая наблюдение за Землей, связь и научные исследования.

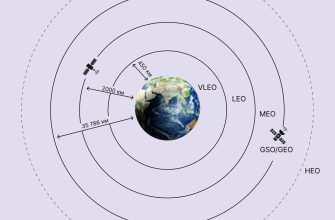
Почему же наклонные орбиты так важны? Во-первых, они позволяют спутникам охватывать большую часть поверхности Земли, в т.ч. и полярные регионы, которые недоступны для спутников на геостационарных орбитах. Во-вторых, наклонные орбиты могут быть оптимизированы для выполнения конкретных задач, таких как наблюдение за определенными территориями или обеспечение связи в определенной области. В-третьих, использование наклонных орбит позволяет снизить энергетические затраты на запуск спутника по сравнению с запуском на геостационарную орбиту.

Основные параметры наклонной орбиты

Для точного расчета траекторий спутников на наклонных орбитах необходимо учитывать ряд ключевых параметров. Вот некоторые из них:

• Наклонение (i): Угол между плоскостью орбиты и плоскостью экватора.
• Большая полуось (a): Половина наибольшего диаметра эллиптической орбиты.
• Эксцентриситет (e): Мера отклонения орбиты от идеальной окружности.
• Долгота восходящего узла (Ω): Угол между точкой весеннего равноденствия и восходящим узлом (точкой, где спутник пересекает плоскость экватора, двигаясь с юга на север).
• Аргумент перигея (ω): Угол между восходящим узлом и перигеем (ближайшей к Земле точкой орбиты).
• Истинная аномалия (ν): Угол между перигеем и текущим положением спутника на орбите.

Понимание этих параметров необходимо для определения положения спутника в пространстве в любой момент времени. Кроме того, они позволяют прогнозировать будущую траекторию спутника и корректировать ее при необходимости.

Методы расчета траекторий: от классики к современным подходам

Существует множество методов расчета траекторий для спутников на наклонных орбитах. В своей работе мы использовали как классические методы, основанные на законах Кеплера и Ньютона, так и современные численные методы, позволяющие учитывать различные возмущения, влияющие на движение спутника.

Классические методы расчета

Классические методы расчета траекторий основаны на следующих принципах:

1. Законы Кеплера: Описывают движение планет вокруг Солнца и могут быть применены к движению спутников вокруг Земли.
2. Закон всемирного тяготения Ньютона: Определяет силу гравитационного взаимодействия между двумя телами.
3. Решение дифференциальных уравнений движения: Позволяет определить положение и скорость спутника в любой момент времени, исходя из его начальных условий и действующих сил.

Эти методы позволяют получить аналитические решения, которые достаточно точны для многих практических задач. Однако они не учитывают различные возмущения, такие как гравитационное воздействие Луны и Солнца, сопротивление атмосферы и давление солнечного света.

Численные методы расчета

Численные методы расчета траекторий позволяют учитывать различные возмущения, что делает их более точными по сравнению с классическими методами. Эти методы основаны на дискретизации времени и итеративном решении дифференциальных уравнений движения. Наиболее распространенные численные методы включают:

• Метод Эйлера: Простейший численный метод, но не очень точный.
• Метод Рунге-Кутты: Более точный метод, широко используемый в практике расчета траекторий.
• Метод Верле: Специально разработан для решения задач небесной механики и сохранения энергии.

При использовании численных методов необходимо тщательно выбирать шаг интегрирования, чтобы обеспечить достаточную точность и стабильность решения. Кроме того, важно учитывать все значимые возмущения, влияющие на движение спутника.

Учет возмущений: ключ к точному прогнозированию

Как мы уже упоминали, учет возмущений является критически важным для точного прогнозирования траекторий спутников на наклонных орбитах. Вот некоторые из наиболее значимых возмущений, которые необходимо учитывать:

• Несферичность Земли: Форма Земли отличается от идеальной сферы, что приводит к дополнительным гравитационным силам, влияющим на движение спутника.
• Гравитационное воздействие Луны и Солнца: Эти тела оказывают гравитационное воздействие на спутник, изменяя его траекторию.
• Сопротивление атмосферы: В верхних слоях атмосферы спутник испытывает сопротивление, которое замедляет его движение и снижает высоту орбиты.
• Давление солнечного света: Фотоны солнечного света оказывают давление на спутник, изменяя его скорость и направление движения.

Для учета этих возмущений необходимо использовать сложные математические модели и численные методы. Кроме того, важно иметь точные данные о параметрах Земли, Луны, Солнца и атмосферы.

Наш опыт в борьбе с возмущениями

В своей работе мы столкнулись с множеством проблем, связанных с учетом возмущений. Например, при расчете траекторий спутников на низких околоземных орбитах, сопротивление атмосферы оказывало существенное влияние на точность прогнозирования. Чтобы решить эту проблему, мы использовали модели атмосферы, основанные на данных с метеорологических спутников и наземных станций. Это позволило нам значительно повысить точность расчета траекторий.

Еще одной проблемой было учет гравитационного воздействия Луны и Солнца. Для этого мы использовали теорию возмущений, которая позволяет представить движение спутника как сумму невозмущенного движения и малых возмущений, вызванных гравитационным воздействием других тел. Этот подход позволил нам получить достаточно точные результаты без чрезмерных вычислительных затрат.

Программное обеспечение для расчета траекторий

Для расчета траекторий спутников на наклонных орбитах мы использовали различное программное обеспечение, как коммерческое, так и разработанное нами самостоятельно. Коммерческое программное обеспечение, такое как STK (Satellite Tool Kit), предоставляет широкий набор инструментов для моделирования космических миссий, включая расчет траекторий, анализ видимости и планирование операций.

Однако, в некоторых случаях, нам требовалось более гибкое и специализированное программное обеспечение, которое бы учитывало особенности нашей конкретной задачи. Поэтому мы разработали собственный программный код на языке Python с использованием библиотек NumPy, SciPy и Matplotlib. Это позволило нам реализовать собственные алгоритмы расчета траекторий и визуализации результатов.

Пример использования Python для расчета траекторий

Вот пример простого кода на Python, который демонстрирует расчет траектории спутника с использованием метода Эйлера:

import numpy as np
import matplotlib.pyplot as plt
# Параметры спутника
a = 7000 # Большая полуось (км)
e = 0.01 # Эксцентриситет
i = np.radians(60) # Наклонение (градусы)
omega = np.radians(30) # Аргумент перигея (градусы)
Omega = np.radians(45) # Долгота восходящего узла (градусы)

# Гравитационный параметр Земли
mu = 398600 # км^3/с^2

# Начальные условия
r0 = np.array([a * (1 ⎯ e), 0, 0]) # Начальное положение
v0 = np.array([0, np.sqrt(mu / a * (1 + e) / (1 ― e)), 0]) # Начальная скорость

# Шаг интегрирования
dt = 10 # секунды

# Время моделирования
t_end = 86400 # секунды (1 день)

# Массивы для хранения результатов
t = np.arange(0, t_end, dt)
r = np.zeros((len(t), 3))
v = np.zeros((len(t), 3))

# Начальные значения
r[0] = r0
v[0] = v0

# Метод Эйлера
for n in range(len(t) ⎯ 1):
# Вычисление гравитационного ускорения
r_norm = np.linalg.norm(r[n])
a_grav = -mu / r_norm*3 r[n]

# Обновление скорости и положения
v[n+1] = v[n] + a_grav * dt
r[n+1] = r[n] + v[n] * dt

# Визуализация результатов
plt.figure(figsize=(10, 6))
plt.plot(r[:, 0], r[:, 1])
plt.xlabel(‘X (км)’)
plt.ylabel(‘Y (км)’)
plt.title(‘Траектория спутника (Метод Эйлера)’)
plt.grid(True)
plt.show

Этот код представляет собой упрощенный пример и не учитывает возмущения. Однако он демонстрирует основные принципы расчета траекторий с использованием Python.

Расчет траекторий для спутников на наклонных орбитах – это сложная, но выполнимая задача. Наш опыт показывает, что для достижения точных результатов необходимо учитывать множество факторов, включая параметры орбиты, возмущения и используемые методы расчета. Важно постоянно совершенствовать свои знания и навыки, а также использовать современные программные инструменты.

Мы надеемся, что эта статья была полезной и вдохновит вас на новые свершения в области космонавтики. Удачи вам в ваших исследованиях и разработках!

Подробнее

Спутниковые траектории	Наклонные орбиты	Расчет орбит	Космическая механика	Прогнозирование траекторий
Оптимизация орбит	Воздействия на орбиты	Программное обеспечение для расчета орбит	Параметры орбит	Моделирование космических миссий