Расчет траекторий для спутников на наклонных орбитах: Наш опыт и секреты

Приветствуем вас, уважаемые читатели! Сегодня мы погрузимся в захватывающий мир космической механики и поговорим о расчете траекторий для спутников, обращающихся вокруг Земли по наклонным орбитам․ Это сложная, но невероятно интересная задача, с которой нам приходилось сталкиваться неоднократно в нашей работе․ Мы поделимся с вами нашим опытом, трудностями, с которыми мы сталкивались, и, конечно же, секретами успешного расчета;

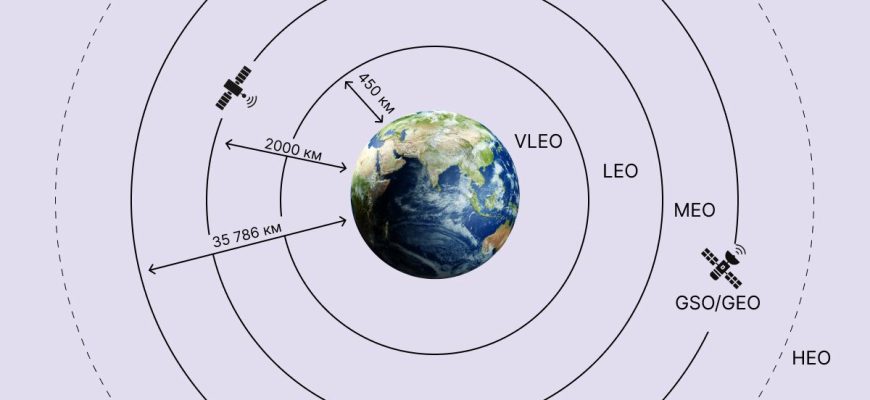
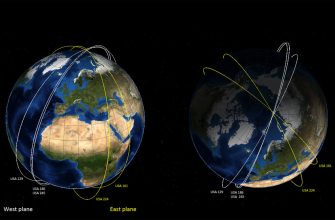
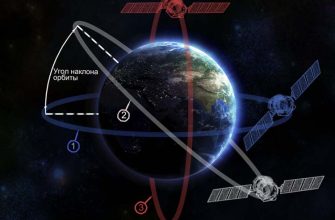
Зачем вообще нужны наклонные орбиты? Ответ кроется в потребностях глобального покрытия и оптимизации задач, возлагаемых на спутники․ В отличие от геостационарных спутников, которые "висят" над одной точкой Земли, спутники на наклонных орбитах обеспечивают покрытие более широких областей, включая приполярные регионы․ Это критически важно для многих приложений, таких как связь, наблюдение за Землей и научные исследования․

Основы расчета траекторий

Прежде чем мы углубимся в детали расчета траекторий наклонных орбит, давайте вспомним основные понятия․ Траектория спутника определяется несколькими ключевыми параметрами, известными как элементы орбиты․ К ним относятся большая полуось, эксцентриситет, наклонение, долгота восходящего узла, аргумент перигея и истинная аномалия․ Каждый из этих параметров играет важную роль в определении положения спутника в пространстве и его движения во времени․

Расчет траекторий основан на законах Кеплера и законах Ньютона о всемирном тяготении․ Однако, в реальности, на движение спутника влияют множество дополнительных факторов, таких как гравитационные аномалии Земли, атмосферное сопротивление и давление солнечного света․ Учет этих факторов значительно усложняет расчет, но является необходимым для достижения высокой точности․

Учет возмущений

Как мы уже упоминали, идеализированная модель движения спутника, основанная только на законах Кеплера, не дает точного представления о реальной траектории․ Возбуждения, вызванные различными факторами, приводят к отклонениям от идеальной орбиты․ Разберем основные из них:

• Гравитационные аномалии Земли: Земля не является идеально сферическим телом, и ее гравитационное поле неоднородно․ Это приводит к возмущениям, особенно заметным для спутников на низких орбитах․
• Атмосферное сопротивление: На низких орбитах спутники испытывают сопротивление со стороны атмосферы, что приводит к постепенному снижению высоты орбиты и изменению ее формы․
• Давление солнечного света: Фотоны солнечного света оказывают небольшое, но ощутимое давление на спутник, что также влияет на его траекторию․
• Притяжение Луны и Солнца: Гравитационное воздействие этих небесных тел также вносит свой вклад в возмущения орбиты спутника․

Для учета возмущений используются различные математические модели и численные методы․ Одним из наиболее распространенных подходов является использование уравнений Лагранжа или уравнений Гаусса, которые позволяют рассчитать изменения элементов орбиты под воздействием возмущающих сил․

Выбор системы координат

Выбор правильной системы координат является критически важным для расчета траекторий․ Существует несколько стандартных систем координат, используемых в космической механике, таких как:

1. Инерциальная система координат: Это система координат, не вращающаяся относительно далеких звезд․ Она используется в качестве базовой системы для описания движения спутника․
2. Земная система координат: Это система координат, связанная с вращающейся Землей․ Она удобна для определения положения спутника относительно поверхности Земли․
3. Орбитальная система координат: Это система координат, связанная с орбитой спутника․ Она удобна для анализа возмущений орбиты․

Преобразование координат между различными системами является неотъемлемой частью процесса расчета траекторий․

Численные методы расчета

В большинстве случаев, уравнения, описывающие движение спутника с учетом возмущений, не имеют аналитических решений․ Поэтому для расчета траекторий используются численные методы․ К наиболее распространенным численным методам относятся:

• Метод Эйлера: Это самый простой численный метод, но он обладает низкой точностью и не подходит для долгосрочного прогнозирования траекторий․
• Метод Рунге-Кутты: Это более точный численный метод, который широко используется для расчета траекторий спутников․ Существуют различные варианты метода Рунге-Кутты, отличающиеся порядком точности․
• Метод Адамса: Это многошаговый численный метод, который может быть более эффективным, чем метод Рунге-Кутты, для некоторых задач․

Выбор численного метода зависит от требуемой точности и вычислительных ресурсов․ Важно также учитывать шаг интегрирования, который влияет на точность и стабильность численного решения․ Слишком большой шаг интегрирования может привести к неустойчивости, а слишком маленький ⎼ к чрезмерным вычислительным затратам․

Наш опыт: Трудности и решения

В нашей практике мы сталкивались с различными трудностями при расчете траекторий для спутников на наклонных орбитах․ Одной из основных проблем является обеспечение высокой точности прогнозирования траекторий на длительный период времени․ Накопление ошибок, вызванных неточностями в моделях возмущений и численными методами, может привести к существенным отклонениям от реальной траектории․

Для решения этой проблемы мы применяем следующие подходы:

• Использование высокоточных моделей гравитационного поля Земли: Мы используем современные модели гравитационного поля, такие как EGM2008, которые учитывают детальную структуру гравитационных аномалий․
• Учет атмосферного сопротивления: Мы разрабатываем модели атмосферного сопротивления, адаптированные к конкретным условиям полета спутника․ Мы используем данные о плотности атмосферы, полученные с помощью спутниковых измерений и наземных наблюдений․
• Калибровка траекторий по данным телеметрических измерений: Мы регулярно калибруем расчетные траектории по данным телеметрических измерений, полученных от спутника․ Это позволяет нам корректировать параметры моделей и повышать точность прогнозирования․
• Использование ансамблевых методов: Мы используем несколько численных методов и моделей возмущений, чтобы получить ансамбль траекторий․ Анализ ансамбля позволяет оценить неопределенность в прогнозировании и улучшить надежность результатов․

Еще одной трудностью является оптимизация траекторий для достижения конкретных целей․ Например, может потребоваться оптимизировать траекторию для обеспечения максимального времени наблюдения за определенной областью Земли или для минимизации расхода топлива при коррекции орбиты․ Для решения этих задач мы используем методы оптимизации, такие как генетические алгоритмы и методы градиентного спуска․

Практические примеры

Чтобы лучше понять, как применяются методы расчета траекторий на практике, рассмотрим несколько примеров:

1. Спутник дистанционного зондирования Земли: Для спутников дистанционного зондирования Земли важно обеспечить регулярное и точное покрытие заданной области․ Расчет траекторий должен учитывать требования к углу обзора и времени прохождения над интересующей областью․
2. Спутник связи: Для спутников связи важно обеспечить устойчивую связь с наземными станциями․ Расчет траекторий должен учитывать требования к видимому углу и дальности связи․
3. Спутник навигации: Для спутников навигации, таких как GPS и ГЛОНАСС, требуется высокая точность определения положения․ Расчет траекторий должен учитывать все возможные возмущения и калиброваться по данным наземных станций․

В каждом из этих случаев расчет траекторий является сложной и многогранной задачей, требующей глубоких знаний в области космической механики, математического моделирования и численных методов․

Будущее расчетов траекторий

Развитие технологий и науки не стоит на месте․ В будущем мы видим следующие тенденции в области расчета траекторий для спутников:

• Более точные модели гравитационного поля Земли и атмосферы: Новые миссии и исследования позволят получить более точные данные о гравитационном поле Земли и плотности атмосферы, что приведет к повышению точности расчетов траекторий․
• Использование методов машинного обучения: Методы машинного обучения могут быть использованы для построения более точных моделей возмущений и для оптимизации траекторий․
• Развитие вычислительных мощностей: Развитие вычислительных мощностей позволит использовать более сложные численные методы и модели для расчета траекторий․
• Автоматизация процесса расчета траекторий: Автоматизация процесса расчета траекторий позволит снизить трудозатраты и повысить эффективность работы․

Мы уверены, что будущее расчетов траекторий будет связано с развитием новых технологий и методов, которые позволят нам более точно и эффективно управлять движением космических аппаратов․

Надеемся, наш опыт был вам полезен! Мы продолжим делиться с вами интересными и полезными статьями о космической механике и других областях науки и техники․

Подробнее

Оптимизация орбит спутников	Прогнозирование положения спутника	Влияние солнечной активности на траекторию	Методы коррекции орбит	Точность расчета траекторий
Моделирование гравитационного поля Земли	Атмосферное торможение спутников	Численные методы в космической механике	Наклонные орбиты: преимущества и недостатки	Программное обеспечение для расчета траекторий