Расчет траекторий для спутников на наклонных орбитах: Путешествие в космос, не вставая с дивана

Когда мы смотрим на ночное небо, усыпанное звездами, вряд ли задумываемся о том, какая сложная работа стоит за тем, чтобы эти светящиеся точки – спутники – выполняли свои задачи. Они передают нам телевизионный сигнал, помогают ориентироваться на местности и даже предсказывают погоду. Но как они оказываются именно там, где должны быть? Все дело в точном расчете траекторий, особенно для спутников, вращающихся по наклонным орбитам.

В этой статье мы погрузимся в увлекательный мир космической механики и расскажем о том, как происходит расчет траекторий спутников на наклонных орбитах. Мы рассмотрим основные принципы, формулы и инструменты, которые используют ученые и инженеры для того, чтобы наши космические аппараты успешно выполняли свои миссии. Приготовьтесь к захватывающему путешествию, которое позволит вам взглянуть на космос под новым углом!

Основы космической механики: Что нужно знать перед расчетом траекторий

Прежде чем приступить к сложным расчетам, важно понимать фундаментальные принципы, лежащие в основе движения спутников. Здесь на сцену выходят законы Кеплера и закон всемирного тяготения Ньютона. Они являются краеугольным камнем космической механики и позволяют нам описывать и предсказывать движение небесных тел.

Первый закон Кеплера: Орбиты планет (и спутников) являются эллипсами, в одном из фокусов которых находится Солнце (или Земля).
Второй закон Кеплера: Радиус-вектор, соединяющий планету (или спутник) с Солнцем (или Землей), заметает равные площади за равные промежутки времени. Это означает, что спутник движется быстрее, когда находится ближе к Земле, и медленнее, когда находится дальше.
Третий закон Кеплера: Квадрат периода обращения планеты (или спутника) пропорционален кубу большой полуоси ее орбиты. Это позволяет нам связать период обращения спутника с размером его орбиты.

Закон всемирного тяготения Ньютона гласит, что сила притяжения между двумя телами пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Именно эта сила удерживает спутник на орбите вокруг Земли.

Что такое наклонная орбита и чем она отличается от других?

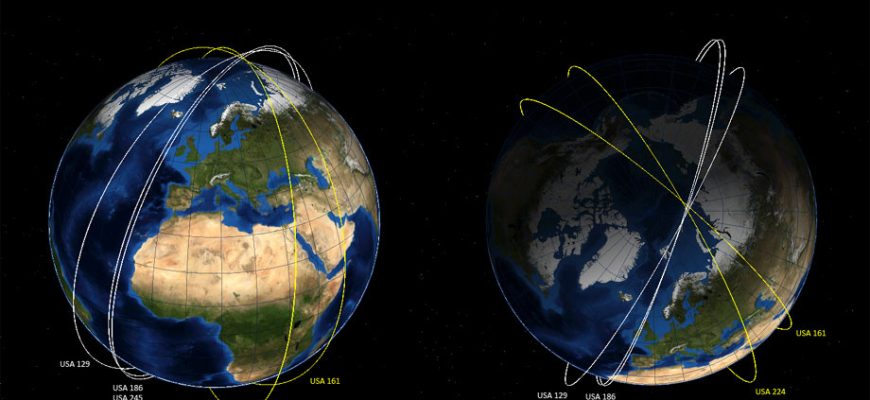
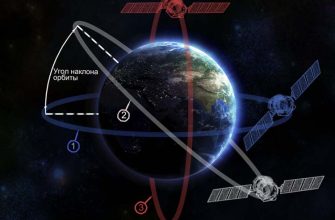
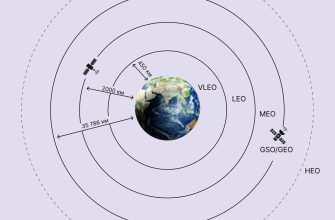
Орбита спутника описывается несколькими параметрами, включая ее наклон. Наклон – это угол между плоскостью орбиты и плоскостью экватора Земли. Если наклон равен 0 градусов, то орбита называется экваториальной, а если 90 градусов – полярной. Орбиты с наклоном, отличным от 0 и 90 градусов, называются наклонными.

Наклонные орбиты обладают рядом преимуществ. Они позволяют спутникам охватывать большую часть земной поверхности, чем экваториальные орбиты. Кроме того, они могут быть выбраны таким образом, чтобы обеспечить наилучшие условия для выполнения конкретных задач, таких как наблюдение за определенными регионами или обеспечение связи в высоких широтах.

Однако, расчет траекторий для спутников на наклонных орбитах более сложен, чем для спутников на экваториальных или полярных орбитах. Это связано с тем, что на движение спутника оказывают влияние различные возмущающие факторы, такие как гравитационное поле Земли, притяжение Луны и Солнца, а также сопротивление атмосферы.

Факторы, влияющие на траекторию спутника на наклонной орбите

Как мы уже упоминали, на траекторию спутника влияют различные факторы. Рассмотрим наиболее важные из них:

Гравитационное поле Земли: Земля не является идеальным шаром, и ее гравитационное поле неоднородно. Это приводит к тому, что орбита спутника постоянно меняется.
Притяжение Луны и Солнца: Луна и Солнце также оказывают гравитационное воздействие на спутник, что приводит к дополнительным возмущениям его орбиты.
Сопротивление атмосферы: На низких орбитах спутник испытывает сопротивление атмосферы, что приводит к постепенному снижению его высоты.
Давление солнечного света: Солнечный свет оказывает давление на спутник, что также может приводить к изменению его орбиты.

Учет этих факторов является критически важным для точного расчета траекторий спутников на наклонных орбитах.

"Космос – это не просто место, где мы можем побывать. Это вызов, который заставляет нас становиться лучше."

— Нил Армстронг

Методы расчета траекторий: от простых моделей к сложным алгоритмам

Существует множество методов расчета траекторий спутников, от простых аналитических моделей до сложных численных алгоритмов. Выбор конкретного метода зависит от требуемой точности и доступных вычислительных ресурсов.

Аналитические методы

Аналитические методы основаны на упрощенных моделях движения спутника. Они позволяют получить решения в виде формул, которые можно использовать для быстрой оценки траектории. Однако, аналитические методы не учитывают все возмущающие факторы, поэтому их точность ограничена.

Численные методы

Численные методы основаны на решении дифференциальных уравнений движения спутника с помощью компьютера. Они позволяют учитывать все возмущающие факторы и получать более точные результаты. Однако, численные методы требуют больших вычислительных ресурсов и времени.

Наиболее распространенными численными методами являются методы Рунге-Кутты и методы Адамса. Они позволяют с высокой точностью моделировать движение спутника на длительных временных интервалах.

Программное обеспечение для расчета траекторий спутников

Для расчета траекторий спутников используется специализированное программное обеспечение. Существует множество коммерческих и бесплатных программ, которые позволяют моделировать движение спутников с учетом различных возмущающих факторов. Некоторые из них:

STK (Satellite Tool Kit): Коммерческое программное обеспечение, широко используемое в космической индустрии.
GMAT (General Mission Analysis Tool): Бесплатное программное обеспечение, разработанное NASA.
Orekit: Бесплатная библиотека Java для космической механики.

Эти программы позволяют инженерам и ученым моделировать различные сценарии и оптимизировать траектории спутников для достижения наилучших результатов.

Применение расчета траекторий в реальной жизни

Расчет траекторий спутников играет важную роль в различных областях:

Связь: Точный расчет траекторий необходим для обеспечения надежной связи через спутники.
Навигация: Спутниковые навигационные системы, такие как GPS и ГЛОНАСС, используют точный расчет траекторий для определения местоположения пользователей.
Наблюдение Земли: Спутники наблюдения Земли используются для мониторинга окружающей среды, сельского хозяйства и других областей. Точный расчет траекторий позволяет получать высококачественные изображения и данные.
Научные исследования: Спутники используются для проведения научных исследований в космосе. Точный расчет траекторий позволяет ученым проводить эксперименты в заданных условиях.

Будущее расчета траекторий: новые технологии и вызовы

В будущем расчет траекторий спутников будет становиться все более важным, поскольку количество спутников на орбите Земли продолжает расти. Новые технологии, такие как искусственный интеллект и машинное обучение, будут использоваться для оптимизации траекторий и повышения точности расчетов.

Одним из главных вызовов является проблема космического мусора. Неработающие спутники и другие объекты, находящиеся на орбите, могут представлять опасность для действующих спутников. Точный расчет траекторий космического мусора необходим для предотвращения столкновений и обеспечения безопасности космической деятельности.

Расчет траекторий спутников на наклонных орбитах – это сложная, но увлекательная область науки и техники. Благодаря точному расчету траекторий мы можем использовать спутники для решения широкого круга задач, от обеспечения связи и навигации до мониторинга окружающей среды и проведения научных исследований. Космос становится ближе, и мы продолжаем исследовать его с помощью все более совершенных технологий.

Подробнее

Орбитальная механика	Спутниковая навигация	Космический мусор	Наклон орбиты	Программное обеспечение для расчета траекторий
Законы Кеплера	Моделирование траекторий	Воздействие на спутник	Оптимизация траекторий	Космические миссии