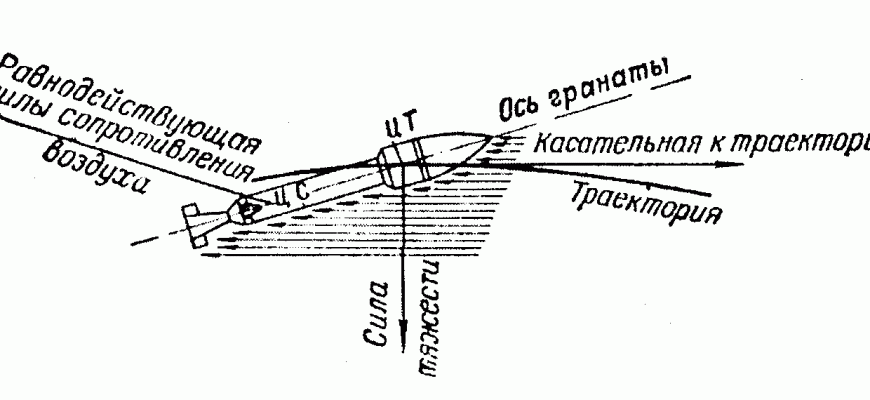
Расчет траекторий с учетом аэродинамических сил: Погружение в мир баллистики

Как часто мы задумываемся о том, что стоит за полетом мяча, выпущенной стрелы или даже космического корабля? Все эти движения, кажущиеся такими простыми, подчиняются сложным законам физики, а их траектории формируются под воздействием множества факторов. Сегодня мы погрузимся в увлекательный мир расчета траекторий, особое внимание уделив влиянию аэродинамических сил – тех самых невидимых, но ощутимых препятствий, с которыми сталкиваются все движущиеся объекты.

Мы, как энтузиасты, увлеченные моделированием и анализом движения, не раз сталкивались с необходимостью точного прогнозирования траекторий. От разработки игр до проектирования спортивного оборудования, от анализа полета дронов до оптимизации баллистических расчетов – везде требуется учитывать аэродинамику. И этот опыт побудил нас поделиться своими знаниями и практическими советами с вами.

Основы баллистики: От идеального мира к реальности

В самом начале изучения баллистики мы часто сталкиваемся с упрощенными моделями, где пренебрегают сопротивлением воздуха. В этих "идеальных" условиях траектория объекта описывается простой параболой, а расчеты сводятся к применению нескольких базовых формул. Однако, как только мы выходим за рамки учебника и сталкиваемся с реальным миром, все становится гораздо сложнее.

Аэродинамические силы – это те самые "возмущения", которые превращают идеальную параболу в кривую, подвластную множеству факторов. Сопротивление воздуха, подъемная сила, вращение объекта – все это влияет на траекторию и требует более сложных математических моделей для точного прогнозирования. Именно поэтому учет аэродинамики является ключевым элементом в любой задаче, связанной с движением тел в атмосфере.

Ключевые аэродинамические силы: Сопротивление и подъемная сила

Две основные силы, с которыми сталкивается движущийся объект в воздухе, – это сопротивление и подъемная сила. Сопротивление, как следует из названия, направлено против движения и замедляет объект. Подъемная сила, напротив, направлена перпендикулярно потоку воздуха и может как поддерживать объект в воздухе (как в случае с крылом самолета), так и отклонять его траекторию.

Величина этих сил зависит от множества факторов: формы объекта, его скорости, плотности воздуха, коэффициентов сопротивления и подъемной силы. Определение этих коэффициентов – отдельная и весьма сложная задача, требующая либо экспериментальных исследований в аэродинамической трубе, либо использования сложных вычислительных методов.

Факторы, влияющие на аэродинамические силы

Как мы уже упоминали, на величину аэродинамических сил влияет целый ряд факторов. Вот лишь некоторые из них:

• Форма объекта: Обтекаемая форма уменьшает сопротивление, а плоская – увеличивает;
• Скорость: Сопротивление воздуха обычно растет пропорционально квадрату скорости.
• Плотность воздуха: Чем плотнее воздух, тем больше сопротивление. Плотность воздуха зависит от температуры, давления и влажности.
• Коэффициенты сопротивления и подъемной силы: Эти коэффициенты зависят от формы объекта и угла атаки (угла между направлением движения и продольной осью объекта).
• Вращение объекта: Вращение может создавать дополнительную подъемную силу (эффект Магнуса).

Математическое моделирование траекторий: От простого к сложному

Для расчета траекторий с учетом аэродинамических сил необходимо использовать математические модели, описывающие движение объекта под воздействием этих сил. Существует множество подходов к моделированию, от простых аналитических решений до сложных численных методов.

Простейшие модели, как правило, предполагают постоянные аэродинамические коэффициенты и пренебрегают изменением плотности воздуха с высотой. Более сложные модели учитывают эти факторы и могут даже включать в себя влияние ветра и других атмосферных явлений. Выбор подходящей модели зависит от требуемой точности и доступных вычислительных ресурсов.

Основные уравнения движения

В основе любого расчета траектории лежат уравнения движения, которые связывают ускорение, скорость и положение объекта. С учетом аэродинамических сил эти уравнения принимают следующий вид:

F = ma

Где:

• F – суммарная сила, действующая на объект (включая силу тяжести, сопротивление воздуха и подъемную силу).
• m – масса объекта.
• a – ускорение объекта.

Решение этих уравнений позволяет определить скорость и положение объекта в любой момент времени. Однако, из-за сложности уравнений, аналитическое решение часто невозможно, и приходится прибегать к численным методам.

Численные методы расчета траекторий

Численные методы позволяют приближенно решать уравнения движения, разбивая время на небольшие интервалы и вычисляя положение и скорость объекта на каждом шаге. Существует множество численных методов, отличающихся по точности и вычислительной сложности. Наиболее распространенные из них – метод Эйлера, метод Рунге-Кутты и метод Верле.

Выбор численного метода зависит от требуемой точности и доступных вычислительных ресурсов. Более точные методы, как правило, требуют больше вычислительного времени, поэтому необходимо находить компромисс между точностью и скоростью расчета.

Практические примеры: От спорта до космоса

Расчет траекторий с учетом аэродинамических сил находит применение в самых разных областях. Рассмотрим несколько практических примеров:

• Спорт: Анализ траектории полета мяча в футболе, гольфе или бейсболе позволяет оптимизировать технику удара и повысить точность броска.
• Авиация: Расчет траектории полета самолета или дрона позволяет планировать маршрут, экономить топливо и избегать столкновений.
• Баллистика: Расчет траектории пули или ракеты позволяет определить дальность и точность стрельбы.
• Космонавтика: Расчет траектории космического корабля или спутника позволяет планировать миссии, выводить аппараты на орбиту и осуществлять посадку на другие планеты.

Пример 1: Расчет траектории футбольного мяча

Представьте себе футбольный матч. Игрок бьет по мячу, и тот летит к воротам. Чтобы точно предсказать, куда приземлится мяч, необходимо учесть не только силу удара и угол вылета, но и сопротивление воздуха, вращение мяча и даже направление ветра. Моделирование траектории футбольного мяча – сложная задача, требующая учета множества факторов, но она позволяет тренерам и игрокам анализировать технику удара и разрабатывать стратегии игры.

Пример 2: Оптимизация траектории дрона

Дроны становятся все более популярными в различных областях, от доставки посылок до мониторинга окружающей среды. Для эффективного использования дронов необходимо оптимизировать их траектории, учитывая сопротивление воздуха, ветер и энергопотребление. Расчет траекторий позволяет дронам летать дальше, быстрее и экономичнее.

Инструменты и программное обеспечение: В помощь исследователю

К счастью, для расчета траекторий с учетом аэродинамических сил существует множество инструментов и программного обеспечения, которые значительно упрощают эту задачу. От бесплатных онлайн-калькуляторов до мощных коммерческих пакетов, каждый может найти подходящий инструмент для своих нужд.

Среди наиболее популярных инструментов можно выделить:

1. MATLAB: Мощная среда для численных расчетов и моделирования.
2. Python: Язык программирования с широким набором библиотек для научных вычислений, таких как NumPy и SciPy.
3. OpenFOAM: Открытый пакет для вычислительной гидродинамики (CFD), позволяющий моделировать движение жидкостей и газов.
4. Online-калькуляторы: Простые инструменты для быстрого расчета траекторий в различных условиях.

Создание собственной модели траектории

Если вы хотите углубиться в тему и получить полный контроль над процессом расчета, вы можете создать собственную модель траектории с использованием одного из вышеперечисленных инструментов. Это потребует определенных знаний в области физики, математики и программирования, но позволит вам адаптировать модель под свои конкретные задачи и получить более глубокое понимание принципов баллистики.

Расчет траекторий с учетом аэродинамических сил – это сложная, но увлекательная задача, требующая знаний в области физики, математики и вычислительной техники. Однако, благодаря современным инструментам и программному обеспечению, она становится доступной не только профессиональным ученым и инженерам, но и энтузиастам, увлеченным моделированием и анализом движения.

Мы надеемся, что эта статья помогла вам разобраться в основных принципах расчета траекторий и вдохновила на дальнейшие исследования в этой захватывающей области. Помните, что практика – лучший способ усвоить теорию, поэтому не бойтесь экспериментировать, создавать свои модели и делиться своими результатами с другими.

Подробнее

Аэродинамическое сопротивление	Подъемная сила	Баллистическая траектория	Численное моделирование	Уравнения движения
Коэффициент сопротивления	Влияние ветра на траекторию	Расчет траектории пули	Моделирование полета мяча	Аэродинамика дронов