Расчет траекторий спутников на наклонных орбитах: от теории к практике

Как разработчикам‚ нам часто приходится сталкиваться с задачами‚ которые кажутся невероятно сложными на первый взгляд. Одной из таких задач‚ с которой мы столкнулись‚ был расчет траекторий спутников‚ движущихся по наклонным орбитам. Это не просто математическая головоломка‚ это задача‚ имеющая огромное практическое значение для навигации‚ связи и научных исследований.

В этой статье мы поделимся нашим опытом‚ начиная с основ теории и заканчивая практическими советами по реализации алгоритмов расчета. Мы расскажем о том‚ какие сложности возникают на этом пути‚ и как мы их преодолевали. Надеемся‚ наш опыт будет полезен всем‚ кто интересуется космической навигацией и расчетом орбит.

Основы теории: что нужно знать о наклонных орбитах

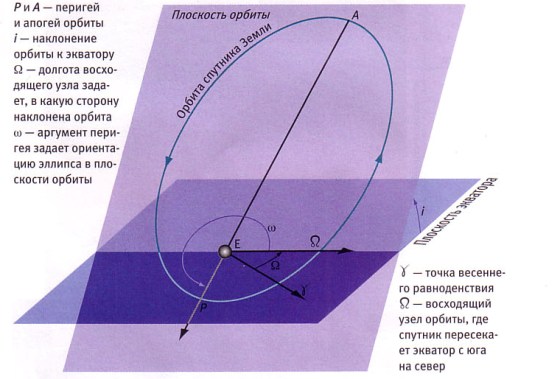
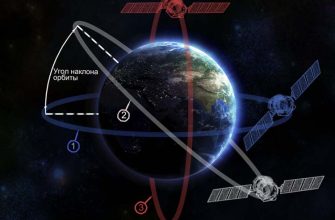
Прежде чем погрузиться в детали расчетов‚ необходимо разобраться в основных понятиях‚ связанных с наклонными орбитами. Орбита спутника – это не просто кружок вокруг Земли. Она описывается множеством параметров‚ которые определяют ее форму‚ размер и положение в пространстве. Один из важнейших параметров – это наклонение.

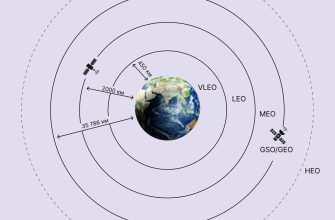
Наклонение – это угол между плоскостью орбиты и плоскостью экватора Земли. Орбиты с наклонением 0 градусов называются экваториальными‚ а орбиты с наклонением 90 градусов – полярными. Все остальные орбиты‚ имеющие угол наклонения от 0 до 90 градусов или от 90 до 180 градусов‚ называются наклонными. Наклонные орбиты позволяют спутникам охватывать большую часть поверхности Земли‚ что делает их особенно полезными для задач наблюдения и связи.

Нам также нужно учитывать‚ что орбиты не идеальны. Они подвержены различным возмущениям‚ вызванным гравитационным воздействием Луны и Солнца‚ несферичностью Земли и другими факторами. Эти возмущения могут существенно влиять на траекторию спутника‚ поэтому их необходимо учитывать при расчетах.

Ключевые параметры орбиты

Для полного описания орбиты спутника нам потребуются следующие параметры:

• Большая полуось (a): определяет размер орбиты.
• Эксцентриситет (e): определяет форму орбиты (0 – круг‚ 1 – парабола).
• Наклонение (i): угол между плоскостью орбиты и плоскостью экватора.
• Долгота восходящего узла (Ω): угол между точкой весеннего равноденствия и восходящим узлом (точкой‚ где спутник пересекает плоскость экватора‚ двигаясь с юга на север).
• Аргумент перигея (ω): угол между восходящим узлом и перигеем (точкой орбиты‚ ближайшей к Земле).
• Средняя аномалия (M): угол‚ который равномерно увеличивается со временем и используется для определения положения спутника на орбите.

Все эти параметры взаимосвязаны и изменяются со временем под воздействием различных возмущений. Для точного расчета траектории необходимо учитывать эти изменения.

Математические модели: от Кеплера до современных алгоритмов

В основе расчета траекторий спутников лежат законы Кеплера‚ сформулированные еще в XVII веке. Эти законы описывают движение планет вокруг Солнца‚ но они также применимы и к движению спутников вокруг Земли.

Первый закон Кеплера гласит‚ что планеты движутся по эллиптическим орбитам‚ в одном из фокусов которых находится Солнце. Второй закон Кеплера утверждает‚ что отрезок‚ соединяющий планету и Солнце‚ заметает равные площади за равные промежутки времени. Третий закон Кеплера устанавливает связь между периодом обращения планеты и размером ее орбиты.

Однако законы Кеплера справедливы только в идеальном случае‚ когда на спутник действует только гравитационное поле Земли. В реальности необходимо учитывать различные возмущения‚ которые усложняют расчеты. Для учета этих возмущений используются различные математические модели и алгоритмы.

Модели возмущений

Существует множество моделей возмущений‚ отличающихся по сложности и точности. Некоторые из наиболее распространенных моделей включают:

• Модель J2: учитывает влияние второй зональной гармоники гравитационного поля Земли‚ которая возникает из-за несферичности планеты.
• Модель SGP4/SDP4: используется для расчета траекторий спутников на низких околоземных орбитах и учитывает влияние атмосферного торможения.
• Модель IERS: включает в себя различные поправки‚ связанные с вращением Земли и движением полюсов.

Выбор модели зависит от требуемой точности расчета и характеристик орбиты спутника; Для высокоточных расчетов необходимо использовать более сложные модели‚ учитывающие больше факторов.

Практическая реализация: разработка программного обеспечения

После того‚ как мы разобрались с теорией и математическими моделями‚ пришло время перейти к практике – разработке программного обеспечения для расчета траекторий спутников. Это сложный и многоэтапный процесс‚ требующий глубоких знаний в области программирования‚ математики и космической навигации.

Мы использовали язык программирования Python‚ благодаря его богатой библиотеке математических функций и инструментов для работы с данными. Мы также использовали библиотеки NumPy и SciPy для выполнения численных расчетов и решения дифференциальных уравнений.

Этапы разработки

1. Импорт данных: загрузка исходных данных об орбите спутника (параметры Кеплера‚ время эпохи).
2. Преобразование координат: преобразование координат из одной системы в другую (например‚ из инерциальной системы в геоцентрическую).
3. Расчет возмущений: вычисление возмущений‚ действующих на спутник‚ с использованием выбранной модели.
4. Интегрирование уравнений движения: численное интегрирование уравнений движения спутника с учетом возмущений.

Каждый из этих этапов требует тщательной проработки и тестирования. Мы потратили много времени на отладку кода и проверку точности расчетов.

Сложности и решения: наш опыт и советы

В процессе разработки мы столкнулись с множеством сложностей. Одной из главных проблем была точность расчетов. Даже небольшие ошибки в исходных данных или алгоритмах могли привести к существенным отклонениям траектории.

Для повышения точности мы использовали методы адаптивного интегрирования‚ которые автоматически регулируют шаг интегрирования в зависимости от требуемой точности. Мы также использовали методы фильтрации Калмана для оценки и коррекции ошибок в исходных данных.

Еще одной сложностью была вычислительная сложность алгоритмов. Расчет траекторий спутников требует выполнения большого количества численных операций‚ что может занимать много времени. Для ускорения расчетов мы использовали методы параллельного программирования и оптимизации кода.

Советы начинающим разработчикам

• Начните с основ: изучите теорию и математические модели‚ прежде чем приступать к разработке.
• Используйте библиотеки: не изобретайте велосипед‚ используйте готовые библиотеки для выполнения численных расчетов и решения дифференциальных уравнений.
• Тщательно тестируйте код: проверяйте точность расчетов на различных примерах и сравнивайте результаты с другими источниками.
• Оптимизируйте код: используйте методы параллельного программирования и оптимизации кода для ускорения расчетов.
• Не бойтесь экспериментировать: пробуйте разные подходы и методы‚ чтобы найти наиболее эффективное решение.

Применение: где используются расчеты траекторий спутников

Расчет траекторий спутников имеет широкое применение в различных областях‚ включая:

• Навигация: определение местоположения и скорости мобильных объектов с использованием спутниковых навигационных систем‚ таких как GPS и ГЛОНАСС.
• Связь: обеспечение связи между удаленными точками на Земле с использованием спутниковых систем связи.
• Наблюдение: получение изображений и данных о поверхности Земли с использованием спутников дистанционного зондирования.
• Научные исследования: изучение космического пространства и атмосферы Земли с использованием научных спутников.
• Управление космическими аппаратами: планирование и выполнение маневров для изменения орбиты и ориентации космических аппаратов.

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
Параметры кеплера	Возможные возмущения орбит	Математические модели орбит	Наклонение орбиты спутника	Расчет эфемерид спутника
Прогнозирование орбит	Элементы орбит	Алгоритмы расчета траекторий	Модели гравитационного поля	Точность расчета орбит