Расчет траекторий: Танцы с гравитацией, или Как предсказать полет сквозь звездные поля

Приветствую, друзья! Сегодня мы погрузимся в захватывающий мир расчета траекторий, но не простых, а с учетом коварного влияния посторонних тел. Представьте себе, что мы – не строгие ученые в белых халатах, а скорее, опытные навигаторы, прокладывающие курс корабля через бушующее море гравитационных волн. И поверьте, это путешествие будет полно неожиданных поворотов и сложных вычислений.

Мы, как и многие, начинали с простых задач: бросок мяча, полет стрелы. Но чем дальше мы углублялись в эту область, тем яснее становилось, что реальный мир гораздо сложнее, чем идеализированные модели из учебников физики. Сторонние тела – будь то планеты, звезды или даже космический мусор – вносят свои коррективы в траекторию движения, превращая её из прямой линии в замысловатую кривую.

Зачем учитывать влияние сторонних тел?

Вопрос резонный. Зачем усложнять себе жизнь, если можно ограничиться расчетом траектории в вакууме, где на тело действует только гравитация центрального объекта? Ответ прост: точность. Если речь идет о навигации космических аппаратов, о предсказании траекторий астероидов или о запуске спутников на околоземную орбиту, даже небольшая ошибка в расчетах может привести к катастрофическим последствиям.

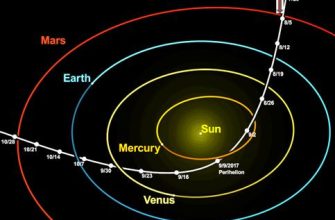
Представьте себе космический аппарат, летящий к Марсу. Небольшая ошибка в расчете траектории, вызванная неучтенным влиянием гравитации Юпитера, может привести к тому, что аппарат промахнется мимо цели на миллионы километров. Или, что еще хуже, столкнется с астероидом, о существовании которого мы даже не подозревали. Поэтому, учет влияния сторонних тел – это не просто академический интерес, а жизненная необходимость.

Методы расчета траекторий

Численное интегрирование

Это, пожалуй, самый распространенный и универсальный метод. Суть его заключается в том, что мы разбиваем время движения тела на небольшие интервалы и на каждом интервале вычисляем силу, действующую на тело со стороны всех гравитирующих объектов. Затем, используя законы Ньютона, определяем изменение скорости и положения тела на этом интервале. Повторяя эту процедуру многократно, мы получаем приближенную траекторию движения.

Численное интегрирование – это как шаг за шагом прокладывать себе путь через лес, ориентируясь по компасу и карте. Чем меньше шаг, тем точнее будет наша траектория, но тем больше времени потребуется на расчет. Существует множество различных методов численного интегрирования, отличающихся по точности и вычислительной сложности. Например, методы Рунге-Кутты, методы Адамса и методы Верле. Выбор конкретного метода зависит от требуемой точности и доступных вычислительных ресурсов.

Метод возмущений

Этот метод основан на предположении, что влияние сторонних тел на траекторию движения относительно невелико. Мы начинаем с расчета траектории в отсутствие посторонних тел, а затем рассматриваем влияние посторонних тел как "возмущение" этой траектории. Метод возмущений позволяет получить аналитическое решение, которое описывает траекторию движения в виде математической формулы.

Представьте себе пловца, плывущего по течению реки. Основное движение определяется течением реки, но на пловца также действуют небольшие возмущения, вызванные ветром, волнами и другими пловцами. Метод возмущений позволяет оценить влияние этих возмущений на траекторию движения пловца. Этот метод особенно эффективен, когда необходимо быстро оценить влияние посторонних тел на траекторию движения, не прибегая к сложным численным расчетам.

Метод эфемерид

Этот метод основан на использовании готовых таблиц, содержащих информацию о положении и скорости небесных тел в разные моменты времени. Эти таблицы называются эфемеридами. Используя эфемериды, мы можем определить положение и скорость сторонних тел в любой момент времени и рассчитать их гравитационное воздействие на движущееся тело.

Представьте себе карту звездного неба, на которой указано положение всех звезд и планет в разные моменты времени. Используя эту карту, мы можем определить положение любого небесного тела в любой момент времени и использовать эту информацию для расчета траектории движения. Метод эфемерид – это как использовать GPS-навигатор для определения своего местоположения и прокладки маршрута. Этот метод особенно удобен, когда необходимо быстро и точно определить траекторию движения в реальном времени.

"Математика ‒ царица наук, а арифметика ‒ царица математики." ― Карл Фридрих Гаусс

Факторы, влияющие на точность расчетов

Даже самые совершенные методы расчета траекторий не гарантируют абсолютной точности. Существует множество факторов, которые могут повлиять на результаты расчетов. К ним относятся:

Неточность исходных данных: Ошибки в определении положения и скорости небесных тел, а также в определении их масс, могут привести к значительным ошибкам в расчетах траектории.
Неучет всех гравитирующих объектов: В реальном мире на движущееся тело действует гравитация не только крупных планет и звезд, но и более мелких объектов, таких как астероиды и кометы. Неучет этих объектов может привести к ошибкам в расчетах.
Релятивистские эффекты: Вблизи массивных объектов, таких как Солнце, необходимо учитывать релятивистские эффекты, описываемые общей теорией относительности. Пренебрежение этими эффектами может привести к ошибкам в расчетах.
Влияние атмосферы: При движении в атмосфере планеты на тело действует сила сопротивления, которая зависит от плотности атмосферы и скорости движения тела. Неучет этой силы может привести к ошибкам в расчетах траектории.
Вычислительные ошибки: Численные методы расчета траекторий неизбежно связаны с вычислительными ошибками, которые могут накапливаться и приводить к значительным погрешностям в результатах.

Применение расчетов траекторий

Расчет траекторий с учетом влияния сторонних тел находит широкое применение в различных областях науки и техники. Вот лишь несколько примеров:

Космическая навигация: Расчет траекторий космических аппаратов, летящих к другим планетам или звездам.
Астрономия: Предсказание траекторий астероидов и комет, а также изучение их движения под влиянием гравитации планет.
Баллистика: Расчет траекторий снарядов и ракет.
Метеорология: Предсказание траекторий движения воздушных масс и циклонов.
Геодезия: Определение положения и скорости искусственных спутников Земли.

Пример расчета траектории

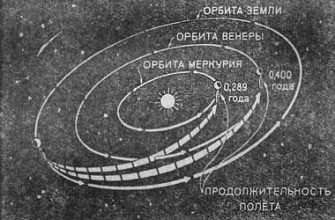
Давайте рассмотрим упрощенный пример расчета траектории космического аппарата, летящего от Земли к Марсу, с учетом гравитационного воздействия Солнца и Юпитера. Мы будем использовать метод численного интегрирования.

Определяем начальные условия: Положение и скорость космического аппарата в момент старта с Земли.
Определяем положение и скорость Солнца и Юпитера: Используем эфемериды для определения положения и скорости Солнца и Юпитера в каждый момент времени.
Рассчитываем гравитационные силы: Рассчитываем гравитационные силы, действующие на космический аппарат со стороны Солнца и Юпитера.
Интегрируем уравнение движения: Используем метод численного интегрирования для решения уравнения движения космического аппарата и определения его положения и скорости в следующий момент времени.
Повторяем шаги 2-4: Повторяем шаги 2-4 до тех пор, пока космический аппарат не достигнет окрестностей Марса.

Этот пример, конечно, очень упрощенный, но он позволяет понять основные принципы расчета траекторий с учетом влияния сторонних тел. В реальности расчеты гораздо сложнее и требуют использования мощных компьютеров и специализированного программного обеспечения.

Расчет траекторий с учетом влияния сторонних тел – это сложная, но увлекательная задача, требующая глубоких знаний в области математики, физики и астрономии. Мы надеемся, что эта статья помогла вам немного приоткрыть завесу тайны над этой областью и вдохновила на дальнейшее изучение.

Мы, как и вы, всегда стремимся к новым знаниям и открытиям. И мы верим, что вместе мы сможем покорить самые отдаленные уголки Вселенной. Удачи вам в ваших исследованиях!

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
гравитационное взаимодействие тел	численные методы расчета траекторий	метод возмущений небесной механики	эфемериды планет солнечной системы	точность расчета космических траекторий
космическая навигация и траектории	влияние Юпитера на траектории	релятивистские поправки траектории	прогнозирование движения астероидов	алгоритмы расчета траекторий