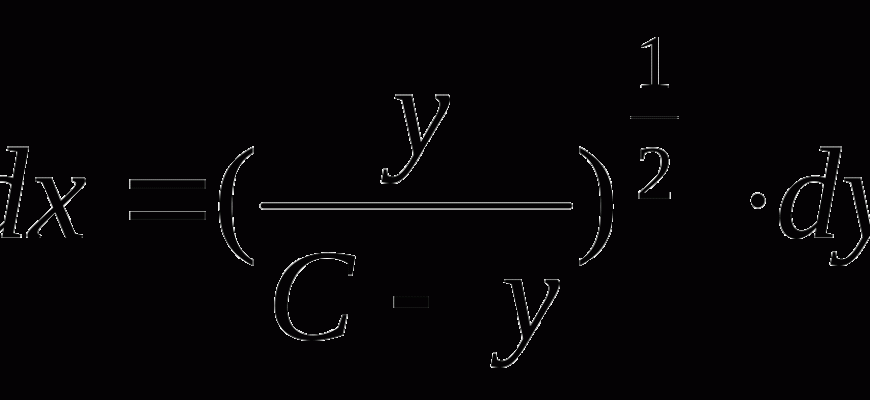Вариационное исчисление: Путь к оптимальному управлению, открытый личным опытом

Мы, как и многие, в начале своего пути к пониманию оптимального управления чувствовали себя немного потерянными. Сложные формулы, абстрактные концепции… казалось, что это удел избранных, гениев математики. Но, шаг за шагом, погружаясь в теорию и практику вариационного исчисления, мы поняли, что это мощный инструмент, доступный каждому, кто готов потратить время и усилия на его освоение; Наш личный опыт подсказывает, что это путешествие стоит затраченных усилий.

В этой статье мы поделимся своим опытом применения вариационного исчисления для решения задач оптимального управления. Мы расскажем о том, с чего начинали, какие трудности встречали на пути, и как их преодолевали. Наша цель – сделать этот сложный материал более понятным и доступным для широкой аудитории.

Что такое вариационное исчисление и зачем оно нужно?

Вариационное исчисление – это раздел математики, занимающийся поиском экстремумов функционалов. Функционал, в отличие от функции, принимает в качестве аргумента не число, а функцию, и возвращает число. Представьте себе, что у вас есть множество возможных траекторий движения объекта, и вам нужно найти ту, которая минимизирует время, затраченное на перемещение. Или, например, вам нужно спроектировать форму моста, которая обеспечит максимальную прочность при минимальном расходе материала. Именно такие задачи и решает вариационное исчисление.

В контексте оптимального управления вариационное исчисление позволяет находить оптимальные управляющие воздействия, которые минимизируют или максимизируют заданный критерий качества. Этот критерий может быть связан с затратами ресурсов, временем выполнения операции, точностью достижения цели и т.д. Применение вариационного исчисления позволяет существенно улучшить характеристики управляемых систем, повысить их эффективность и надежность.

Основные понятия и принципы

Прежде чем углубляться в детали, давайте рассмотрим основные понятия и принципы вариационного исчисления:

• Функционал: Отображение, которое ставит в соответствие каждой функции некоторое число. Например, интеграл от функции на заданном интервале.
• Экстремум функционала: Максимум или минимум значения функционала на некотором множестве функций.
• Вариация функции: Бесконечно малое изменение функции.
• Уравнение Эйлера-Лагранжа: Основное уравнение вариационного исчисления, которое позволяет найти функции, доставляющие экстремум функционалу.
• Граничные условия: Условия, которые должны выполняться на концах интервала, на котором рассматривается функционал.

Эти понятия кажутся сложными, но на практике, при решении конкретных задач, они становятся более понятными и наглядными. Главное – не бояться экспериментировать и пробовать разные подходы.

Наш первый опыт: Простейшая задача вариационного исчисления

Мы начали свое знакомство с вариационным исчислением с решения простейшей задачи – задачи о брахистохроне. Эта задача была сформулирована Иоганном Бернулли в 1696 году и звучит так: найти кривую, соединяющую две заданные точки, по которой материальная точка, двигаясь только под действием силы тяжести, достигнет нижней точки за наименьшее время.

Решение этой задачи потребовало от нас изучения основ вариационного исчисления, освоения метода Эйлера-Лагранжа и навыков решения дифференциальных уравнений. Это был сложный, но очень полезный опыт. Мы поняли, как применять теоретические знания на практике, и увидели, как вариационное исчисление позволяет находить оптимальные решения в конкретных задачах.

Шаг за шагом: Решение задачи о брахистохроне

1. Формулировка задачи: Определяем функционал, который нужно минимизировать (в данном случае, время движения), и граничные условия (координаты начальной и конечной точек).
2. Составление уравнения Эйлера-Лагранжа: Подставляем функционал в уравнение Эйлера-Лагранжа и получаем дифференциальное уравнение, которое описывает оптимальную траекторию.
3. Решение дифференциального уравнения: Решаем полученное дифференциальное уравнение с учетом граничных условий. Решение оказывается циклоидой.
4. Анализ результата: Убеждаемся, что полученное решение действительно минимизирует время движения, и анализируем его свойства.

Этот процесс был не всегда гладким. Мы сталкивались с трудностями при решении дифференциальных уравнений, при интерпретации результатов, но благодаря упорству и настойчивости мы смогли успешно решить задачу о брахистохроне. И это дало нам уверенность в своих силах и мотивацию для дальнейшего изучения вариационного исчисления.

Применение вариационного исчисления в оптимальном управлении

После успешного решения задачи о брахистохроне мы решили применить вариационное исчисление для решения задач оптимального управления. Нас интересовали задачи управления движением, управления технологическими процессами и управления экономическими системами.

Мы обнаружили, что вариационное исчисление является мощным инструментом для решения широкого круга задач оптимального управления. Оно позволяет находить оптимальные управляющие воздействия, которые минимизируют или максимизируют заданный критерий качества, и обеспечивает высокую эффективность и надежность управляемых систем.

Примеры задач оптимального управления

• Управление движением: Оптимальное управление траекторией движения робота, автомобиля, самолета или космического аппарата.
• Управление технологическими процессами: Оптимальное управление температурой, давлением, расходом вещества в химическом реакторе или другом технологическом процессе.
• Управление экономическими системами: Оптимальное управление инвестициями, производством, запасами и другими экономическими переменными.

Решение каждой из этих задач требует индивидуального подхода, но общая методология остается той же: формулировка задачи, составление функционала, применение уравнения Эйлера-Лагранжа, решение дифференциального уравнения и анализ результата.

Трудности и как мы их преодолевали

На пути освоения вариационного исчисления и его применения в оптимальном управлении мы столкнулись с рядом трудностей. Некоторые из них были связаны с математическим аппаратом, другие – с практической реализацией полученных решений.

• Сложность математического аппарата: Вариационное исчисление требует хорошего знания математического анализа, дифференциальных уравнений и других разделов математики. Мы решали эту проблему путем углубленного изучения теории и практики, а также путем консультаций с более опытными коллегами.
• Сложность решения дифференциальных уравнений: Уравнение Эйлера-Лагранжа часто приводит к сложным дифференциальным уравнениям, которые не всегда удается решить аналитически. Мы использовали численные методы решения дифференциальных уравнений, а также специализированное программное обеспечение.
• Практическая реализация полученных решений: Оптимальные решения, полученные с помощью вариационного исчисления, не всегда удается реализовать на практике из-за ограничений, связанных с физическими свойствами системы, точностью измерений и другими факторами. Мы учитывали эти ограничения при формулировке задачи и при разработке алгоритмов управления;

Преодоление этих трудностей потребовало от нас упорства, настойчивости и готовности к постоянному обучению. Но мы уверены, что это был ценный опыт, который помог нам стать более квалифицированными специалистами в области оптимального управления.

Советы начинающим

Основываясь на своем опыте, мы хотели бы дать несколько советов начинающим изучать вариационное исчисление и его применение в оптимальном управлении:

• Начните с основ: Изучите основные понятия и принципы вариационного исчисления, такие как функционал, экстремум функционала, вариация функции, уравнение Эйлера-Лагранжа.
• Решайте задачи: Решайте как можно больше задач, начиная с простых и постепенно переходя к более сложным. Это поможет вам закрепить теоретические знания и развить практические навыки.
• Используйте программное обеспечение: Используйте специализированное программное обеспечение для решения дифференциальных уравнений, численного интегрирования и визуализации результатов.
• Не бойтесь обращаться за помощью: Если у вас возникли трудности, не стесняйтесь обращаться за помощью к более опытным коллегам или преподавателям.
• Будьте настойчивы: Изучение вариационного исчисления требует времени и усилий. Не отчаивайтесь, если что-то не получается сразу. Будьте настойчивы, и вы обязательно добьетесь успеха.

Вариационное исчисление – это мощный инструмент для решения задач оптимального управления. Оно позволяет находить оптимальные управляющие воздействия, которые минимизируют или максимизируют заданный критерий качества, и обеспечивает высокую эффективность и надежность управляемых систем. Наш личный опыт показал, что освоение этого инструмента требует времени и усилий, но это того стоит. Мы надеемся, что наша статья поможет вам на вашем пути к пониманию и применению вариационного исчисления.

Мы верим, что вариационное исчисление сыграет важную роль в развитии науки и техники в будущем, и призываем всех, кто интересуется оптимальным управлением, изучать и применять этот мощный инструмент.

Подробнее

Вариационное исчисление применение	Оптимальное управление примеры	Функционал определение	Уравнение Эйлера-Лагранжа вывод	Брахистохрона решение
Методы оптимального управления	Экстремум функционала	Принцип оптимальности Беллмана	Задача оптимального управления линейным объектом	Вариационное исчисление учебник