Искусство Предвидения: Как Оценить Точность Прогнозов Траектории

В мире‚ где каждое решение требует предвидения‚ умение прогнозировать траекторию – будь то курс акций‚ движение логистики или даже развитие карьеры – становится бесценным навыком. Мы‚ как исследователи и практики‚ постоянно сталкиваемся с необходимостью оценки точности этих прогнозов. Ведь просто сделать прогноз недостаточно; критически важно понимать‚ насколько мы можем ему доверять. Эта статья – наш личный опыт и руководство по методам определения ошибок в прогнозировании траекторий‚ основанное на реальных кейсах и проверенных подходах.

Почему Оценка Ошибок Прогноза Так Важна?

Представьте себе ситуацию: вы разрабатываете систему автоматической навигации для беспилотного автомобиля. Точность прогноза траектории – это вопрос жизни и смерти; Или‚ например‚ вы инвестируете в стартап‚ основываясь на прогнозах роста рынка. Ошибка в этих прогнозах может привести к значительным финансовым потерям. В каждом из этих сценариев цена ошибки может быть очень высокой. Поэтому‚ прежде чем принимать решения‚ основанные на прогнозах‚ необходимо тщательно оценить их точность и понять‚ какие факторы могут повлиять на результат.

Мы пришли к выводу‚ что понимание потенциальных ошибок прогноза позволяет:

• Принимать более обоснованные решения.
• Минимизировать риски.
• Оптимизировать стратегии.
• Повысить доверие к прогностическим моделям.

Основные Методы Оценки Ошибок Прогноза

Среднеквадратическая Ошибка (MSE) и Корень из Среднеквадратической Ошибки (RMSE)

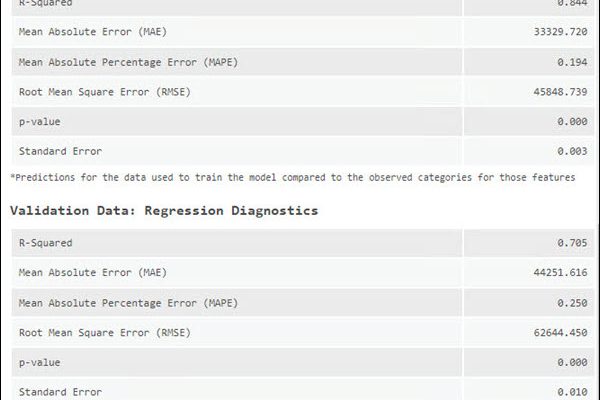
MSE (Mean Squared Error) – это один из самых распространенных методов оценки точности прогнозов. Он вычисляет среднее значение квадратов разностей между прогнозируемыми и фактическими значениями. Квадратичная функция штрафует большие ошибки сильнее‚ чем маленькие‚ что делает MSE чувствительным к выбросам.

RMSE (Root Mean Squared Error) – это просто корень квадратный из MSE. Он возвращает ошибку в тех же единицах измерения‚ что и исходные данные‚ что облегчает интерпретацию результатов.

Формула MSE: MSE = (1/n) * Σ(yi ー ŷi)2‚ где y_i ⎼ фактическое значение‚ ŷ_i ー прогнозируемое значение‚ n ー количество наблюдений.

Формула RMSE: RMSE = √MSE

Пример: Предположим‚ мы прогнозируем продажи товара на неделю. Фактические продажи составили 10‚ 12‚ 15‚ 13‚ 16 единиц. Наши прогнозы были 9‚ 11‚ 14‚ 14‚ 15 единиц. Вычисляем MSE и RMSE:

1. Разности: 1‚ 1‚ 1‚ -1‚ 1
2. Квадраты разностей: 1‚ 1‚ 1‚ 1‚ 1
3. MSE: (1+1+1+1+1)/5 = 1
4. RMSE: √1 = 1

В данном случае‚ RMSE равен 1‚ что означает‚ что в среднем наш прогноз отклоняется от фактических продаж на 1 единицу.

Средняя Абсолютная Ошибка (MAE)

MAE (Mean Absolute Error) – это среднее значение абсолютных разностей между прогнозируемыми и фактическими значениями. В отличие от MSE‚ MAE менее чувствителен к выбросам‚ так как не использует квадратичную функцию.

Формула MAE: MAE = (1/n) * Σ|yi ー ŷi|

Преимущества MAE:

• Простота интерпретации.
• Устойчивость к выбросам.

Недостатки MAE:

• Не дифференцируема в точке 0‚ что может быть проблемой для некоторых алгоритмов оптимизации.

Средняя Абсолютная Процентная Ошибка (MAPE)

MAPE (Mean Absolute Percentage Error) – это среднее значение абсолютных процентных разностей между прогнозируемыми и фактическими значениями. MAPE выражает ошибку в процентах‚ что облегчает сравнение точности прогнозов для разных масштабов данных.

Формула MAPE: MAPE = (1/n) * Σ(|(yi ー ŷi) / yi|) * 100%

Важно: MAPE не применим‚ если фактические значения могут быть равны нулю‚ так как это приведет к делению на ноль.

Коэффициент Детерминации (R²)

R² (R-squared) – это мера того‚ насколько хорошо модель объясняет изменчивость данных. Он показывает‚ какая доля дисперсии зависимой переменной объясняется независимыми переменными. R² принимает значения от 0 до 1‚ где 1 означает‚ что модель идеально объясняет данные‚ а 0 – что модель не объясняет ничего.

Формула R²: R2 = 1 ー (Σ(yi ⎼ ŷi)2 / Σ(yi ⎼ ȳ)2)‚ где ȳ ⎼ среднее значение фактических значений.

R² полезен для сравнения различных моделей и оценки их общей пригодности для прогнозирования.

Учет Факторов‚ Влияющих на Точность Прогноза

На точность прогноза траектории влияет множество факторов‚ и игнорирование этих факторов может привести к серьезным ошибкам. Некоторые из наиболее важных факторов включают:

• Качество данных: "Мусор на входе – мусор на выходе". Неточные‚ неполные или устаревшие данные могут значительно ухудшить точность прогноза.
• Выбор модели: Разные модели подходят для разных типов данных и задач. Важно выбрать модель‚ которая наилучшим образом соответствует характеристикам данных и поставленной задаче.
• Параметры модели: Параметры модели необходимо тщательно настраивать‚ чтобы достичь оптимальной производительности.
• Внешние факторы: Внешние факторы‚ такие как экономические условия‚ политические события или погодные условия‚ могут оказать существенное влияние на траекторию.
• Неопределенность: Неопределенность – это неотъемлемая часть любого прогноза. Важно учитывать неопределенность и оценивать диапазон возможных исходов.

Практические Советы по Оценке Ошибок Прогноза

Основываясь на нашем опыте‚ мы можем дать несколько практических советов по оценке ошибок прогноза:

1. Используйте несколько метрик: Не полагайтесь только на одну метрику. Используйте несколько метрик‚ чтобы получить более полное представление о точности прогноза.
2. Визуализируйте результаты: Визуализация результатов прогноза может помочь выявить закономерности и аномалии‚ которые могут быть не видны при использовании только числовых метрик.
3. Проводите перекрестную проверку: Перекрестная проверка (cross-validation) – это метод оценки производительности модели на независимых данных. Она помогает избежать переобучения и получить более надежную оценку точности прогноза.
4. Анализируйте ошибки: Анализируйте ошибки‚ чтобы понять‚ почему модель ошибается и как ее можно улучшить.
5. Учитывайте контекст: Учитывайте контекст задачи и выбирайте метрики и методы оценки‚ которые наилучшим образом соответствуют этому контексту.

Пример Использования Методов Оценки Ошибок Прогноза

Предположим‚ мы разрабатываем модель для прогнозирования трафика на сайте интернет-магазина. Мы используем исторические данные о трафике‚ сезонности и рекламных кампаниях для обучения модели. После обучения модели мы проводим перекрестную проверку и оцениваем точность прогноза с помощью MSE‚ MAE и MAPE. Мы также визуализируем результаты прогноза и анализируем ошибки‚ чтобы понять‚ какие факторы оказывают наибольшее влияние на точность прогноза. На основе этого анализа мы корректируем модель и параметры‚ чтобы улучшить ее производительность.

Оценка ошибок прогноза – это важная часть процесса прогнозирования. Правильная оценка позволяет нам принимать более обоснованные решения‚ минимизировать риски и оптимизировать стратегии. В этой статье мы рассмотрели основные методы оценки ошибок прогноза и дали несколько практических советов по их применению. Надеемся‚ что эта информация поможет вам улучшить точность ваших прогнозов и принимать более успешные решения.

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
Оценка точности прогноза	Методы прогнозирования траектории	Анализ ошибок прогнозов	Среднеквадратическая ошибка MSE	Средняя абсолютная ошибка MAE
MAPE как мера ошибки	Коэффициент детерминации R2	Факторы влияющие на прогноз	Перекрестная проверка прогнозов	Улучшение точности прогноза