Танцы со Звездами: Как Мы Вычисляем Траектории в Космическом Балете

Когда мы смотрим на ночное небо‚ усыпанное мириадами звезд‚ нам кажется‚ что все эти небесные тела застыли в вечном танце. Но на самом деле‚ космос – это арена непрерывного движения‚ где каждый объект‚ от крошечного астероида до гигантской галактики‚ находится под влиянием гравитационных сил. И предсказать‚ куда именно отправится тот или иной космический странник‚ – задача не из легких. Сегодня мы расскажем о том‚ как мы‚ исследователи космоса‚ пытаемся разгадать эти замысловатые траектории‚ учитывая влияние всех окружающих тел.

Погрузимся в мир небесной механики‚ где математика встречается с физикой‚ а сложные уравнения помогают нам заглянуть в будущее космических объектов. Нам предстоит узнать о методах‚ которые позволяют учитывать гравитационное влияние не только центрального тела (например‚ звезды или планеты)‚ но и всех "сторонних" тел‚ которые могут внести свои коррективы в траекторию.

Ньютоновский Подход: Основа Небесной Механики

Все начинается с классической механики‚ с законов‚ сформулированных Исааком Ньютоном. Закон всемирного тяготения‚ пожалуй‚ самый известный из них‚ гласит‚ что любое тело притягивает другое с силой‚ пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Именно этот закон лежит в основе большинства расчетов траекторий. Мы используем его для определения силы гравитационного воздействия между небесными телами.

Однако‚ когда речь идет о расчете траекторий в реальных космических условиях‚ применение закона Ньютона становится не таким уж и простым. Ведь в космосе редко встретишь ситуацию‚ когда на объект воздействует только одно гравитационное поле. Обычно их гораздо больше. И вот тут на сцену выходят более сложные методы.

Проблема N-тел: Когда Двух Тел Недостаточно

Проблема двух тел‚ когда мы рассматриваем взаимодействие только двух объектов‚ имеет аналитическое решение. То есть‚ мы можем вывести формулу‚ которая описывает траекторию движения этих тел. Но стоит добавить третье тело‚ как задача становится невероятно сложной. Именно это и называется "проблемой N-тел"‚ где N – количество взаимодействующих объектов. Для N > 2 аналитического решения не существует.

Что же делать? Как мы справляемся с этой проблемой? Мы прибегаем к численным методам. Это означает‚ что мы разбиваем время на небольшие интервалы и на каждом интервале рассчитываем силы‚ действующие на объект‚ а затем определяем его новое положение и скорость. Повторяя эту процедуру многократно‚ мы можем аппроксимировать траекторию движения объекта;

Численные Методы: Инструменты для Решения Сложных Задач

Существует множество различных численных методов‚ которые мы используем для расчета траекторий. Вот некоторые из наиболее популярных:

Метод Эйлера: Самый простой метод‚ но и наименее точный. Он хорошо подходит для ознакомления с принципами численного интегрирования‚ но для реальных задач его точности обычно недостаточно.
Метод Рунге-Кутты: Более точный метод‚ который использует несколько промежуточных вычислений для оценки положения и скорости объекта. Существуют различные модификации метода Рунге-Кутты‚ отличающиеся порядком точности.
Метод Верле: Метод‚ который особенно хорошо подходит для задач небесной механики‚ так как он сохраняет энергию системы с высокой точностью. Это важно‚ потому что позволяет избежать накопления ошибок в процессе расчета.

Выбор конкретного численного метода зависит от требуемой точности и вычислительных ресурсов. Для задач‚ требующих высокой точности‚ мы используем более сложные методы‚ такие как методы Рунге-Кутты высокого порядка или методы с переменным шагом интегрирования.

Учет Влияния Сторонних Тел: Гравитационный Хаос

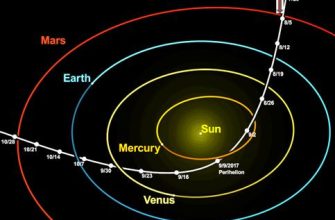
Теперь давайте поговорим о том‚ как мы учитываем влияние сторонних тел. Как мы уже говорили‚ в космосе редко встретишь ситуацию‚ когда на объект действует только одно гравитационное поле. Например‚ при расчете траектории космического аппарата‚ летящего к Марсу‚ необходимо учитывать гравитационное влияние Солнца‚ Земли‚ Марса‚ Юпитера и других планет.

Влияние этих сторонних тел может быть довольно значительным‚ особенно на больших расстояниях. Оно может приводить к изменению траектории‚ скорости и даже к потере аппарата. Поэтому очень важно учитывать это влияние при планировании космических миссий.

Мы учитываем влияние сторонних тел путем добавления соответствующих гравитационных сил в уравнения движения. На каждом шаге численного интегрирования мы рассчитываем силу‚ действующую на объект со стороны каждого стороннего тела‚ и добавляем ее к общей силе. Это позволяет нам получить более точную траекторию движения объекта.

"Наука – это организованное знание. Мудрость – это организованная жизнь."

— Иммануил Кант

Сложности и Ограничения: Когда Математика Сталкивается с Реальностью

Несмотря на все наши усилия‚ расчет траекторий с учетом влияния сторонних тел остается сложной задачей. Существует несколько факторов‚ которые ограничивают нашу точность:

Неточность данных: Мы не всегда знаем точное положение и массу всех небесных тел. Эти данные могут быть неточными или устаревшими‚ что приводит к ошибкам в расчетах.
Вычислительные ресурсы: Расчет траекторий с учетом влияния большого количества сторонних тел требует значительных вычислительных ресурсов. Для задач‚ требующих высокой точности‚ может потребоваться использование суперкомпьютеров.
Хаос: В некоторых случаях траектории движения небесных тел могут быть хаотичными. Это означает‚ что небольшие изменения в начальных условиях могут приводить к большим изменениям в траектории. В таких случаях предсказать траекторию на длительный период времени становится практически невозможным.

Тем не менее‚ мы постоянно работаем над улучшением наших методов и алгоритмов. Мы разрабатываем новые численные методы‚ используем более точные данные и применяем более мощные компьютеры. Это позволяет нам все точнее и точнее предсказывать траектории движения небесных тел.

Применение на Практике: От Космических Миссий до Астероидной Опасности

Зачем нам все это нужно? Зачем мы так тщательно рассчитываем траектории движения небесных тел? Применений этих знаний очень много:

Планирование космических миссий: Расчет траекторий необходим для планирования полетов космических аппаратов к другим планетам‚ спутникам и астероидам. Точный расчет траектории позволяет минимизировать расход топлива и время полета.
Навигация: Расчет траекторий используется для навигации космических аппаратов в процессе полета. С помощью измерений положения и скорости аппарата можно корректировать его траекторию‚ чтобы он достиг заданной цели.
Прогнозирование астероидной опасности: Расчет траекторий астероидов позволяет прогнозировать возможность их столкновения с Землей. Если существует реальная угроза столкновения‚ можно принять меры для предотвращения катастрофы.
Изучение динамики Солнечной системы: Расчет траекторий позволяет изучать динамику Солнечной системы и эволюцию орбит планет и других небесных тел.

Таким образом‚ методы расчета траекторий с учетом влияния сторонних тел играют важную роль в освоении космоса и обеспечении безопасности нашей планеты. Это сложная‚ но увлекательная область науки‚ которая постоянно развивается и открывает новые возможности.

Будущее Небесной Механики: Квантовые Эффекты и Релятивистские Поправки

Мы уже многого достигли в области расчета траекторий небесных тел‚ но впереди еще много работы. В будущем нам предстоит учитывать все более сложные факторы‚ такие как квантовые эффекты и релятивистские поправки. Эти факторы становятся важными при расчете траекторий объектов‚ движущихся с высокой скоростью или находящихся вблизи массивных тел.

Кроме того‚ мы будем продолжать разрабатывать новые численные методы и алгоритмы‚ которые позволят нам рассчитывать траектории с еще большей точностью и скоростью. Мы также будем использовать искусственный интеллект и машинное обучение для анализа больших объемов данных и выявления закономерностей в движении небесных тел.

Небесная механика – это динамично развивающаяся область науки‚ которая открывает перед нами все новые горизонты. Мы уверены‚ что в будущем нас ждет еще много интересных открытий и достижений в этой области.

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
гравитационное взаимодействие тел	численные методы в астрономии	проблема трех тел решение	расчет траектории полета	влияние планет на траекторию
моделирование космических орбит	метод Эйлера применение	точность расчета траекторий	гравитационный маневр расчет	астероидная опасность прогнозирование