Укрощение Космоса: Расчет Траекторий в Многотельной Задаче

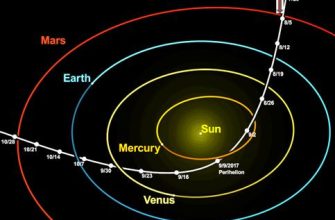
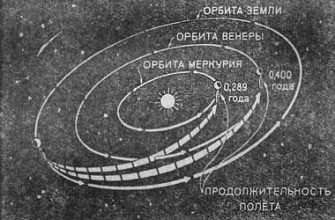
Мы, как и многие исследователи космоса, всегда были очарованы сложностью и красотой движения небесных тел․ Отправляясь в космическое путешествие, будь то мысленное или реальное, необходимо понимать, что на траекторию любого объекта влияют не только гравитация центрального тела (например, Земли или Солнца), но и гравитационное воздействие других планет, спутников, и даже астероидов․ Этот учет "сторонних тел" превращает задачу расчета траекторий из простой в невероятно сложную, но и захватывающую․

В этой статье мы поделимся нашим опытом в этой области, расскажем о методах, которые мы использовали, о трудностях, с которыми столкнулись, и о том, как их преодолевали․ Приготовьтесь к погружению в мир небесной механики, где точность расчетов определяет успех космической миссии․

Основы Расчета Траекторий: Двухтельная Задача

Для начала, давайте вспомним основы․ В простейшем случае, когда мы рассматриваем движение одного тела (например, спутника) вокруг другого (например, Земли), мы имеем дело с так называемой "двухтельной задачей"․ Эта задача имеет аналитическое решение, основанное на законах Кеплера и законе всемирного тяготения Ньютона․ Решение позволяет нам точно определить орбиту спутника, зная его начальное положение и скорость․

Однако, в реальном космосе все гораздо сложнее․ Кроме Земли, на спутник действуют гравитационные силы Луны, Солнца, других планет, а также различные возмущающие факторы, такие как сопротивление атмосферы (на низких орбитах) и давление солнечного света․ Все эти факторы необходимо учитывать для точного расчета траектории․

Многотельная Задача: Когда Простота Уступает Сложности

Когда мы добавляем в нашу модель гравитационное воздействие других тел, задача становится "многотельной"․ В отличие от двухтельной задачи, многотельная задача не имеет аналитического решения в общем виде․ Это означает, что мы не можем получить формулу, которая бы описывала траекторию тела в любой момент времени․ Вместо этого, нам приходится использовать численные методы для приближенного решения․

Суть численных методов заключается в том, что мы разбиваем время на небольшие интервалы и на каждом интервале вычисляем изменение положения и скорости тела под действием гравитационных сил․ Затем, используя эти изменения, мы определяем положение и скорость тела в следующий момент времени․ Повторяя этот процесс много раз, мы можем проследить траекторию тела на протяжении длительного времени․

Методы Численного Интегрирования

Существует множество численных методов для решения многотельной задачи․ Некоторые из наиболее распространенных включают:

• Метод Эйлера: Самый простой метод, но и наименее точный․ Он использует значение производной в начале интервала времени для оценки значения функции в конце интервала;
• Метод Рунге-Кутты: Более точный метод, который использует несколько промежуточных точек внутри интервала времени для оценки значения функции․ Существует несколько вариантов метода Рунге-Кутты, различающихся порядком точности․
• Метод Верле: Метод, специально разработанный для решения задач небесной механики․ Он обладает хорошими свойствами сохранения энергии, что важно для длительного моделирования траекторий․
• Методы предиктор-корректор: Эти методы используют два этапа: предиктор (предсказание значения) и корректор (уточнение значения)․

Выбор конкретного метода зависит от требуемой точности и вычислительных ресурсов․ Для задач, требующих высокой точности, обычно используются методы Рунге-Кутты высокого порядка или методы Верле․

Учет Возмущений: Гравитация и Не Только

Помимо гравитационного воздействия других тел, на траекторию космического аппарата могут влиять и другие факторы, такие как:

• Сопротивление атмосферы: На низких орбитах сопротивление атмосферы оказывает значительное влияние на траекторию, замедляя аппарат и снижая его высоту․
• Давление солнечного света: Фотоны солнечного света оказывают небольшое давление на поверхность аппарата, что также может влиять на его траекторию․
• Несферичность Земли: Земля не является идеальной сферой, и ее гравитационное поле имеет сложные вариации, которые необходимо учитывать для точного расчета траекторий․
• Приливные силы: Воздействие Луны и Солнца на форму Земли вызывает приливные силы, которые также влияют на орбиты спутников․

Для учета этих возмущений используются различные модели и методы․ Например, для моделирования сопротивления атмосферы используются модели атмосферы, которые описывают плотность атмосферы в зависимости от высоты, широты, долготы и времени года․ Для учета несферичности Земли используются разложения гравитационного поля в ряд по сферическим функциям․

Наш Опыт: Взлеты и Падения

В процессе расчета траекторий с учетом влияния сторонних тел мы столкнулись с рядом трудностей․ Одной из главных проблем является высокая вычислительная сложность задачи․ Для точного моделирования траекторий на длительное время требуется огромное количество вычислений, что может потребовать значительных вычислительных ресурсов․

Другой проблемой является точность исходных данных․ Для точного расчета траектории необходимо знать с высокой точностью положение и скорость всех тел, влияющих на траекторию․ Однако, точность этих данных ограничена, что приводит к погрешностям в расчетах․

Тем не менее, мы разработали ряд методов и алгоритмов, которые позволяют нам значительно повысить точность и эффективность расчетов․ Одним из ключевых методов является использование адаптивных алгоритмов, которые автоматически изменяют шаг интегрирования в зависимости от требуемой точности․ Это позволяет нам экономить вычислительные ресурсы, не теряя при этом в точности․

Пример из Практики: Моделирование Траектории Спутника на Геостационарной Орбите

Одним из интересных проектов, в которых мы участвовали, было моделирование траектории спутника на геостационарной орбите․ Геостационарная орбита находится на высоте около 36 000 км над Землей, и спутники на этой орбите кажутся неподвижными относительно поверхности Земли․ Эти спутники используются для телекоммуникаций, телевидения и других целей․

Моделирование траектории спутника на геостационарной орбите является сложной задачей, так как на спутник действуют гравитационные силы Солнца и Луны, а также давление солнечного света․ Эти силы приводят к тому, что спутник медленно смещается со своей номинальной позиции, и необходимо периодически корректировать его орбиту с помощью двигателей․

Мы разработали модель, которая учитывает все эти факторы, и использовали ее для прогнозирования смещения спутника и планирования маневров коррекции орбиты․ Результаты моделирования позволили нам значительно снизить расход топлива на коррекцию орбиты и продлить срок службы спутника․

Инструменты и Программное Обеспечение

Для расчета траекторий с учетом влияния сторонних тел мы используем различные инструменты и программное обеспечение․ Некоторые из наиболее важных инструментов включают:

• MATLAB: Мощная среда для численных расчетов и моделирования․ Мы используем MATLAB для разработки и тестирования наших алгоритмов․
• STK (Satellite Tool Kit): Коммерческое программное обеспечение для моделирования космических миссий․ STK предоставляет широкий набор инструментов для расчета траекторий, визуализации данных и анализа производительности миссии․
• SPICE Toolkit: Библиотека, разработанная NASA, для работы с планетарными данными․ SPICE Toolkit предоставляет доступ к точным данным о положении и скорости планет, спутников и других небесных тел․

Кроме того, мы разрабатываем собственные специализированные инструменты и библиотеки для решения конкретных задач․ Эти инструменты позволяют нам автоматизировать процесс расчета траекторий и повысить точность и эффективность расчетов․

Будущее Расчета Траекторий

Область расчета траекторий с учетом влияния сторонних тел продолжает развиваться․ С развитием вычислительной техники и появлением новых алгоритмов мы можем моделировать траектории с все большей точностью и скоростью․ Это открывает новые возможности для исследования космоса и разработки новых космических миссий․

Одним из перспективных направлений является использование машинного обучения для расчета траекторий․ Алгоритмы машинного обучения могут быть обучены на больших объемах данных о траекториях космических аппаратов и использовать эти знания для прогнозирования траекторий в новых ситуациях․ Это может позволить нам значительно ускорить процесс расчета траекторий и повысить его точность․

Другим важным направлением является разработка новых методов управления траекториями космических аппаратов․ Эти методы позволяют нам активно управлять траекторией аппарата, используя двигатели и другие устройства, чтобы достичь желаемой цели․ Это может быть особенно важно для сложных миссий, таких как миссии к другим планетам или миссии по уборке космического мусора․

Подробнее

Численные методы интегрирования траекторий	Влияние гравитации планет на орбиты	Моделирование космических траекторий	Расчет возмущений орбит	Прогнозирование движения космических аппаратов
Анализ стабильности орбит	Оптимизация траекторий космических миссий	Программное обеспечение для расчета траекторий	Методы коррекции орбит	Геостационарные орбиты: расчет и поддержание