За гранью гравитации: Как рассчитывать траектории, когда в игру вступают сторонние тела

Мы всегда восхищались точностью, с которой небесные тела движутся по своим орбитам. Но что происходит, когда на их пути встают другие гравитационные силы? Как рассчитать траекторию космического аппарата, пролетающего мимо нескольких планет? Или как предсказать движение астероида, подверженного влиянию не только Солнца, но и Юпитера? Сегодня мы погрузимся в увлекательный мир небесной механики и расскажем о методах расчета траекторий с учетом влияния сторонних тел, опираясь на наш собственный опыт и исследования.

Ньютоновское притяжение: Основа основ

В основе всего лежит закон всемирного тяготения Ньютона. Он гласит, что сила гравитационного притяжения между двумя телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Звучит просто, но когда речь заходит о трех и более телах, задача становится невероятно сложной. Проблема трех тел, как ее называют, не имеет общего аналитического решения. Это означает, что мы не можем выразить положение и скорость каждого тела в виде простой формулы, зависящей от времени.

Тем не менее, закон Ньютона – это отправная точка. Мы можем использовать его для построения дифференциальных уравнений, описывающих движение каждого тела. Эти уравнения говорят нам, как изменяется скорость тела в каждый момент времени под действием гравитационных сил. Решение этих уравнений – это и есть определение траектории.

Численные методы: Когда аналитика бессильна

Поскольку аналитические решения недоступны, мы прибегаем к численным методам. Они позволяют нам приближенно решать дифференциальные уравнения, разбивая время на небольшие шаги и вычисляя положение и скорость каждого тела на каждом шаге. Существует множество численных методов, каждый со своими достоинствами и недостатками; Например, метод Эйлера прост в реализации, но не очень точен. Методы Рунге-Кутты, напротив, более сложны, но обеспечивают гораздо более высокую точность.

Выбор численного метода зависит от требуемой точности и доступных вычислительных ресурсов. Для простых задач может быть достаточно метода Эйлера, но для моделирования сложных траекторий космических аппаратов, требующих высокой точности, необходимо использовать более продвинутые методы.

Метод Эйлера: Простота и наглядность

Метод Эйлера – один из самых простых численных методов. Он основан на линейной экстраполяции. Мы предполагаем, что скорость тела в течение небольшого промежутка времени остается постоянной и равной скорости в начале этого промежутка. Затем мы вычисляем новое положение тела, умножая скорость на длительность промежутка времени и прибавляя результат к старому положению.

Методы Рунге-Кутты: Точность и надежность

Методы Рунге-Кутты – это семейство численных методов, обеспечивающих более высокую точность, чем метод Эйлера. Они основаны на вычислении нескольких промежуточных значений скорости в течение каждого временного шага и усреднении этих значений для получения более точной оценки скорости в конце шага. Существуют различные порядки методов Рунге-Кутты, каждый из которых обеспечивает различную степень точности. Наиболее распространенным является метод Рунге-Кутты четвертого порядка (RK4).

Проблема N тел: От трех до бесконечности

Мы говорили о проблеме трех тел, но что, если тел больше? Проблема N тел, где N – любое число больше двух, также не имеет общего аналитического решения. Однако численные методы позволяют нам моделировать движение большого количества тел. Например, мы можем моделировать движение тысяч звезд в галактике, учитывая гравитационное взаимодействие между каждой парой звезд.

С ростом числа тел вычислительная сложность задачи быстро возрастает. Для моделирования движения большого количества тел требуются мощные компьютеры и эффективные алгоритмы. Одним из таких алгоритмов является метод "дерева сил", который позволяет приближенно вычислять гравитационные силы, действующие на каждое тело, группируя удаленные тела в "узлы" дерева.

"Геометрия – это не только знание, но и искусство." – Анри Пуанкаре

Факторы, влияющие на точность расчета

Точность расчета траекторий зависит от множества факторов, включая точность исходных данных (массы, положения и скорости тел), выбранный численный метод, величину временного шага и вычислительную мощность компьютера. Чем точнее исходные данные и чем меньше временной шаг, тем выше точность расчета. Однако уменьшение временного шага приводит к увеличению вычислительного времени.

Также важно учитывать релятивистские эффекты, особенно при моделировании движения тел вблизи массивных объектов, таких как черные дыры. В этих случаях необходимо использовать уравнения общей теории относительности Эйнштейна, а не закон всемирного тяготения Ньютона.

Применение расчетов траекторий

Расчеты траекторий с учетом влияния сторонних тел имеют широкое применение в различных областях науки и техники. Они используются:

В астрономии для изучения движения планет, звезд и галактик.
В космонавтике для планирования полетов космических аппаратов.
В баллистике для расчета траекторий снарядов и ракет.
В геодезии для определения формы и размеров Земли.

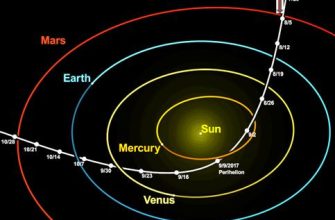
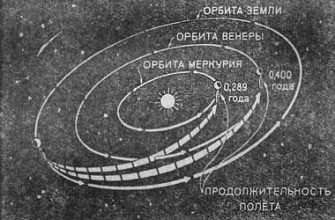
Например, при планировании миссии к Марсу необходимо учитывать гравитационное влияние Земли, Луны, Солнца и других планет. Точный расчет траектории позволяет минимизировать расход топлива и сократить время полета.

Практический пример: Расчет траектории астероида

Предположим, мы хотим рассчитать траекторию астероида, подверженного влиянию Солнца и Юпитера. Для этого нам понадобятся следующие данные:

Масса Солнца и Юпитера.
Начальное положение и скорость астероида.
Положение и скорость Солнца и Юпитера в начальный момент времени.

Затем мы можем использовать численный метод (например, RK4) для решения уравнений движения астероида. На каждом временном шаге мы вычисляем гравитационную силу, действующую на астероид со стороны Солнца и Юпитера, и используем эти силы для определения нового положения и скорости астероида.

Результатом расчета будет траектория астероида, показывающая, как он движется в пространстве под действием гравитационных сил. Мы можем использовать эту траекторию для предсказания будущего положения астероида и оценки вероятности его столкновения с Землей.

Расчет траекторий с учетом влияния сторонних тел – это сложная, но увлекательная задача, требующая глубоких знаний в области небесной механики, математики и программирования. Численные методы являются мощным инструментом, позволяющим нам моделировать движение тел в гравитационных полях и решать задачи, не имеющие аналитических решений. Эти расчеты имеют широкое применение в различных областях науки и техники и позволяют нам лучше понимать окружающий мир.

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
Гравитационное взаимодействие тел	Численное моделирование траекторий	Проблема трех тел решение	Метод Рунге-Кутты применение	Траектория космического аппарата расчет
Влияние Юпитера на астероиды	Закон всемирного тяготения Ньютона	Небесная механика основы	Расчет орбит планет	Определение положения астероида